Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Ia=I12=4A\)
\(Ia1=I1=1A\)
\(=>Ia2=Ia-Ia1=3A\)
\(=>Uv=U2=U1=I2.R2=60\left(V\right)=>R1=\dfrac{U1}{I1}=60\left(om\right)\)

a, ta có I1+I2=I=3(A)
\(I_1=\dfrac{36}{30}=1,2\left(A\right)\)
\(\Rightarrow I_2=3-I_1=1,8\left(A\right)\)
b, \(R_2=\dfrac{U}{I_2}=\dfrac{36}{1,8}=20\left(\Omega\right)\)
\(a,=>R1//R2\)
\(=>Ia=I1+I2=3A\)
\(=>Uv=U1=U2=36V\)
\(=>I1=\dfrac{U1}{R1}=\dfrac{36}{30}=1,2A=Ia1\)
\(=>I2=I1-I1=3-1,2=1,8A=Ia2\)
b, \(=>Rtd=\dfrac{30R2}{30+R2}=\dfrac{U}{Ia}=\dfrac{36}{3}=12=>R2=20\left(om\right)\)

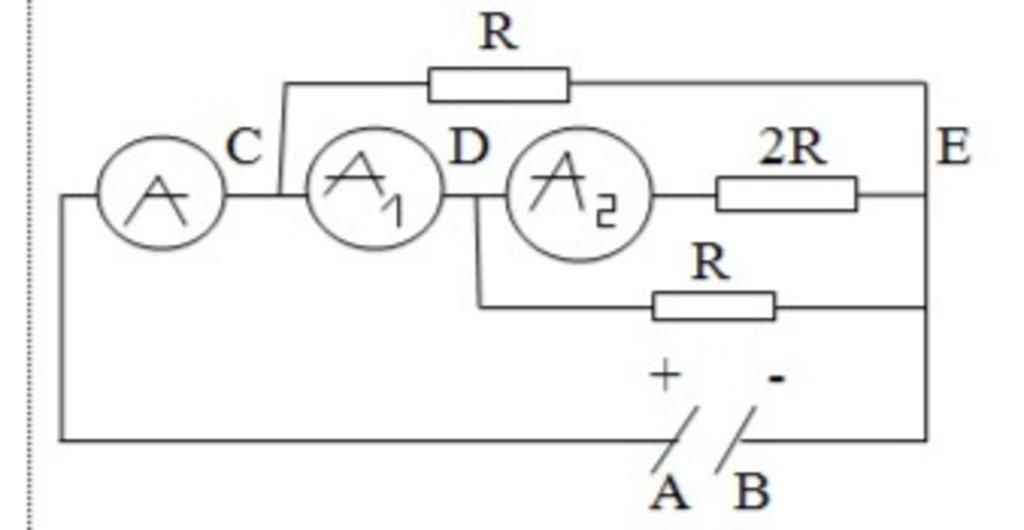
Vì R 1 mắc song song R 2 nên U 1 = U 2 = U V = U M N = 36V
Số chỉ của ampe kế 1 là: 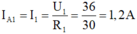
Số chỉ của ampe kế 2 là: 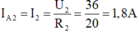

a)R1//R2
\(\dfrac{R_1}{R_2}=\dfrac{I_2}{I_1}=\dfrac{1}{1,5}=\dfrac{2}{3}\)
\(\Rightarrow3R_1=2R_2\)
\(\Leftrightarrow3.20=2R_2\)
\(\Rightarrow R_2=30\Omega\)
Rnt(R1//R2)
\(R_{td}=R+\dfrac{R_1R_2}{R_1+R_2}=10+\dfrac{30.20}{30+20}=22\Omega\)
\(I=I_{12}=1,5+1=2,5\left(A\right)\)
\(U=R_{td}.I=22.2,5=55\left(V\right)\)

Ta có:
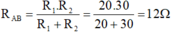
Vì R1 và R2 mắc song song nên U A B = U 1 = U 2 = I A . R A B = 1,2.12 = 14,4 V.
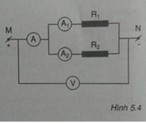
Số chỉ của ampe kế 1 là:
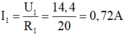
Số chỉ của ampe kế 2 là:
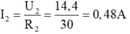

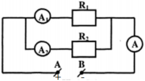
TH1: k1 mở; k2 đóng.
=> Dòng điện đi qua R1:
=> \(R_1=\dfrac{U}{I_{A_1}}=\dfrac{12}{0,2}=60\Omega\)
TH1: k1 đóng; k2 mở.
=> Dòng điện đi qua R3:
=> \(R_3=\dfrac{U}{I_{A_2}}=\dfrac{12}{0,3}=40\Omega\)
a, k1; k2 đóng => A chập C; B chập D R1 R2 R3
Do R1//R2//R3
=> \(U_1=U_2=U_3=U=12\left(V\right)\)
=> \(I=I_1+I_2+I_3\)
<=>\(I_2=I-I_1-I_3=0,6-\dfrac{12}{0,2}-\dfrac{12}{0,3}=0,1\left(A\right)\)
=> \(R_2=\dfrac{U_2}{I_2}=\dfrac{12}{0,1}=120\Omega\)
Chỉ số ampe kế A1 là: \(I_{A_1}=I_3+I_2=\dfrac{U}{R_3}+I_2=0,4\left(A\right)^{\left(1\right)}\)
Chỉ số ampe kế A2 là \(I_{A_2}=I_2+I_1=\dfrac{U}{R_2}+0,1=0,2+0,1=0,3\left(A\right)^{\left(2\right)}\)
b, Ta có: \(A=I_1+I_2+I_3^{\left(3\right)}\)
Từ (1);(2);(3) ta thấy rằng chỉ số của 3 ampe kế đều phụ thuộc vào I2.
=> \(I_2=\dfrac{U}{R_2}=\dfrac{12}{R_2}\); Vậy chỉ cần thay đỗi điện trở R2, chỉ số 3 ampe kế thay đỗi


a) Tính số chỉ \(\dfrac{R}{R_A}\):
I\(_R\) = I\(_{A1}\) - I\(_{A2}\) = 1 - 0,4 = 0,6 (A)
U\(_R\) = 0,6
Ta có: U\(_{DE}\) = ( R\(_A\) + 2R ) . 0,4
Mà: U\(_{DE}\) = U\(_R\)
\(\Leftrightarrow\) 0,6R = ( R\(_A\) + 2R ) . 0,4 \(\Leftrightarrow\) \(\dfrac{R}{R_A}\) = -2
b) hình như đề bài cho A\(_1\)= 1A rồi mà bạn