Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) mạch ((R3//R4)ntR2)//R1=>Rtđ=7,5\(\Omega\)
b) R342//R1=>U324=U1=U
=>I1=\(\dfrac{U}{15}A\)
Vỉ R34ntR2=>I34=I2=\(\dfrac{U}{15}A\)
Vì R3//R4=>U3=U4=U34=I34.R34=\(\dfrac{U}{15}.5=\dfrac{U}{3}V\)=>I3=\(\dfrac{U3}{R3}=\dfrac{U}{3.10}\)
=>I4=\(\dfrac{U4}{10}=\dfrac{U}{3.10}A\)
ta có Ia=I1+I3=3A=>\(\dfrac{U}{15}+\dfrac{U}{30}=3=>U=30V\)
Thay U=30V tính được I1=2A;I2=2A;I4=1A;I3=1A
Vậy........

a) Điện trở tương đương đoạn mạch :
\(R = R_1 + R_2 + R_3 = 20 + 30 + 40 = 90 (\Omega) \quad\)
b) Hiệu điện thế giữa hai đầu AB :
\(U = IR = 0,2 \cdot 90 = 18 (V) \quad\)
c) Do \(R_1 \; nt \; R_2 \; nt \; R_3\) nên \(I_1 = I_2 = I_3 = I = 0,2 (A) \quad\)
Hiệu điện thế giữa hai đầu mỗi điện trở :
\(U_1 = I_1 R_1 = 0,2 \cdot 20 = 4 (V) \quad\)
\(U_2 = I_2 R_2 = 0,2 \cdot 30 = 6 (V) \quad\)
\(U_3 = I_3 R_3 = 0,2 \cdot 40 = 8 (V) \quad\)

a. \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{15.10}{15+10}=6\) (ôm)
\(\Rightarrow R_{tđ}=R_{23}+R_1=6+9=15\)(ôm)
b. Vì \(R_2\)//\(R_3\Rightarrow U_2=U_3\Leftrightarrow15I_2=10I_3\)
\(\Rightarrow I_3=\dfrac{15I_2}{10}=\dfrac{15.0,2}{10}=0,3\)(A)
\(\Rightarrow I_1=I_2+I_3=0,2+0,3=0,5\)(A)
c. ta có \(I=I_1=0,5\)
\(\Rightarrow U=I.R_{tđ}=0,5.15=7,5\)(V)
bn tự tóm tắt nhé
Giải
a,Ta có ( R2//R3)ntR1
nên Rtđ=\(\dfrac{R_2.R_3}{R_2+R_3}+R_1\)=\(\dfrac{15.100}{15+100}+9=\dfrac{507}{23}A\)
b,HĐT giữa hai đầu R2 là :
U2=I2.R2=0,2.15=3V
Ta lại có R2 //R3 =>U2=U3=3V
c đ d đ chạy qua R3 là :
I3=\(\dfrac{U_3}{R_3}=\dfrac{3}{100}=0,03A\)
=> \(I_1=I_2+I_3=0,2+0,03=0,23A\)
c, HĐT giữa 2 đầu R1,R23 là :
U1=I1.R1=0,23.9=2,07V
U23=I23.R23=0,23.\(\dfrac{15.100}{15+100}\)=\(\dfrac{39}{23}V\)
=> UAB = U1+U23=2,07+\(\dfrac{39}{23}\)\(\approx3,766V\)

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

bài này mình giải đk rùi. Mọi người giúp mình các bài còn lại vs. Mai mình cần lắm rùi

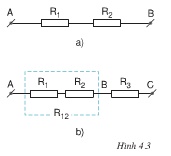
a) Điện trở tương đương của đoạn mạch đó là Rtđ = R1 + R2 = 20 + 20 = 40 Ω.
b) Đoạn mạch mới có ba điện tích mắc nối tiếp nhau, điện trở tương đương của nó là R = R1 + R2 + R3 = 20 + 20 + 20 = 60 Ω.

ta có :
\(R_{t\text{đ}}=\left(\dfrac{R_2\cdot R_3}{R_2+R_3}\right)+R_1\)
\(=\dfrac{R^2}{2R}+R\) =\(=\dfrac{R^2}{2R}+\dfrac{2R^2}{2R}\)=\(\dfrac{3R^2}{2R}\)
Từ đề bài ta có :
\(\dfrac{3R^2}{2R}=120\)
Giải phương trình được:
R = 80Ω
Bài làm:
Sơ đồ mạch điện là: \(\left(R_2\text{/}\text{/}R_3\right)ntR_1\)
Từ sơ đồ mạch điện nên: \(\Rightarrow R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{R^2}{2R}=\dfrac{R}{2}\left(\Omega\right)\)
\(\Rightarrow R_{TĐ}=R_{23}+R_1=\dfrac{R}{2}+R\left(\Omega\right)\)
Mà: \(R_{TĐ}=120\left(\Omega\right)\)
\(\Rightarrow\dfrac{R}{2}+R=120\Rightarrow R=80\left(\Omega\right)\)
Vậy ...................................

Tóm tắt :
\(R_1//R_2\)
R1 = 6Ω
Rtđ = 3Ω
R2 =?
GIẢI :
Cthức : \(R_{tđ}=\frac{R_1R_2}{R_1+R_2}\)
Thay số : \(3=\frac{6.R_2}{6+R_2}\)
\(\Leftrightarrow6R_2=18+3R_2\)
=> A. \(R_2=6\Omega\)

 2
2