Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

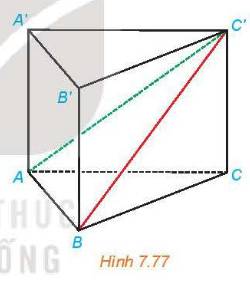
Ta có AA’//(BCC’B’) nên khoảng cách từ AA' đến mặt phẳng (BCC'B') cũng chính là khoảng cách từ A đến mặt phẳng (BCC'B').


Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AA'}=\overrightarrow{c}\)
với \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\)
và \(\left|\overrightarrow{a}\right|=a,\overrightarrow{\left|b\right|}=a\sqrt{2},\left|\overrightarrow{c}\right|=a\sqrt{3}\)
khi đó
\(\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{c,}\overrightarrow{BC}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Giả sử đường vuông góc chung cắt \(\overrightarrow{AB}\) tại M và cắt \(\overrightarrow{BC'}\) tại N và \(\overrightarrow{AM}=x.\overrightarrow{AB'}=x.\overrightarrow{a}+x.\overrightarrow{c},\overrightarrow{BN}=y.\overrightarrow{BC'}=-y.\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Suy ra \(\overrightarrow{AN}=\left(1-y\right)\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Và do đó
\(\overrightarrow{MN}=\left(1-x-y\right)\overrightarrow{a}+y.\overrightarrow{b}+\left(y-x\right)\overrightarrow{c}\)
Ta có :
\(MN\perp AB',BC'\Leftrightarrow\begin{cases}\overrightarrow{MN}.\overrightarrow{AB}=0\\\overrightarrow{MN}.\overrightarrow{BC'}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-4x+2y+1=0\\-2x+6y-1=0\end{cases}\)
Giải hệ ta thu được \(x=\frac{2}{5},y=\frac{3}{10}\)
Từ đó :
\(MN^2=\left[\left(1-x-y\right)^2+2y^2+3\left(y-x\right)^2\right].a^2=\frac{39^a}{100}\)
Suy ra \(d\left(AB';BC'\right)=\frac{a\sqrt{39}}{10}\)

Đáp án B.
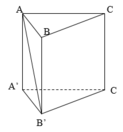
Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có chiều cao AA’; tâm của đáy là trung điểm của AC nên
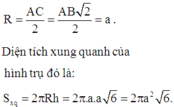

Đáp án A
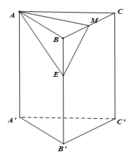
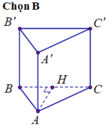
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
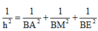
![]()
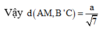

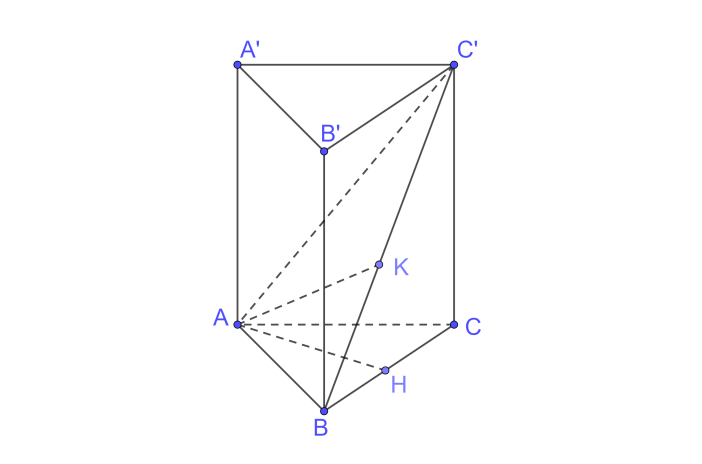
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)

Chọn A.
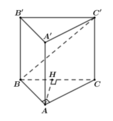
Gọi H là hình chiếu của A lên BC. Ta có
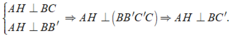
Suy ra AH là đoạn vuông góc chung của AA' và BC' nên
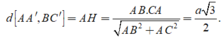

Đáp án D
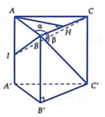
Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()

Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1