Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm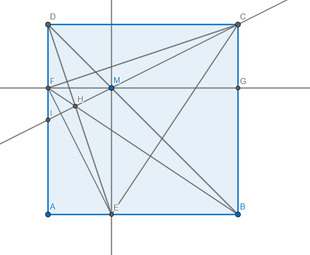

Cậu ơi cho t hỏi tí: câu (a) ấy cái chỗ c/m AD vuông góc vs BC trình bày kiểu gì cho nó logic được ???

Chào người đẹp
a) Dễ quá
b)Quá dễ
c) ko khó
DF = DL => DB là đường trung trực của FL
=> BD vuông góc và chia FL ra 2 đoạn bằng nhau
hay OB vừa đg cao vừa đường trung tuyến
=> tam giác FOL cân
=>OF= OL
=>BLC=90độ
chắn nữa đường tròn
d) dễ quá khỏi làm
d)Gọi Q là giao điểm của (O) và SC
Vì EF song song với BQ (do RSQ=BQC=90)
=>EQ=BF;BF=BL=>EQ=BF=BL
=>góc EBQ=BQL(cùng nhìn 2 cung bằng nhau)
Mà EQ=BL
=>tứ giác BEQL là hình thang cân
=>BQ=EL
mà tứ giác SQBR là hình chữ nhật =>RS=BQ
EL=DE+DL
=>...........
hsg có mấy chỗ tự hiểu
