Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABD và tam giác BDC có:
\(\widehat{BAD}=\widehat{DBC}=90^o\)
\(\widehat{ABD}=\widehat{BDC}\) (Cùng phụ với góc \(\widehat{ADC}\) )
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow BD^2=\frac{AB}{DC}\)
Xét tam giác vuông ABD, áp dụng định lý Pi-ta-go ta có:
\(DB^2=AB^2+AD^2=2^2+4^2=20\)
Suy ra \(2=\frac{20}{DC}\Rightarrow DC=10cm\)
Xét tam giác vuông BDC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=DC^2-BD^2=10^2-20=80\Rightarrow BC=\sqrt{80}\left(cm\right)\)
Vậy chu vi hình thang vuông bằng: 2 + 4 + 10 + \(\sqrt{80}=14+\sqrt{80}\left(cm\right)\)
Diện tích hình thang bằng: \(\frac{\left(2+10\right).4}{2}=24\left(cm^2\right)\)

Bài này mà của lớp 9 thì dễ, lớp 8 thì làm thế này nhé.
Trên AD lấy điểm E sao cho góc ABE=60 độ.
Đặt AB = x (x>0)
Tam giác ABE vuông có góc ABE = 60 độ nên BE = 2 AB = 2x.
Áp dụng định lí Pi-ta-go => AE= \(\sqrt{3}\)x
Tam giác BED cân tại E => BE = ED = 2x.
=> AD = AE + ED =\(\sqrt{3}\)x +2x =x(\(\sqrt{3}\) +2)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD
BD2 = AB2 + AD2 <=> 172 = x2 +(\(\sqrt{3}\)+2)2 x2 => x=\(\frac{17}{\sqrt{8+4\sqrt{3}}}\)
=> AB, AD => Diện tích của hcn ABCD.

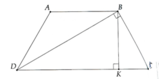
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2

chu vi là 32cm => độ dài các cạnh của hình vuông là :32;4=8(cm)
giả sử đường chèo là BC
áp dụng định lý py ta go ta có
AC2+AB2=BC2
=> 82+82=BC2
=> 128=BC2
hay bình phương độ dì đường chéo là 128 cm
tk mk nha