Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 B
2 A
3 CHỈ CÓ 3 ĐỘ THÔI BẠN LÚC 3 GIỜ 15 PHÚT KIM DÀI CÁCH CHỈ ĐÚNG VÀO SỐ 3 CÒN KIM NGẮN PHẢI TẠO VỚI KIM DÀI 1 GÓC 3 ĐỘ NẾU KHÔNG PHẢI THÌ ĐỒNG HỒ BỊ CHỈNH SỬA RÙI ĐÓ
4 10
5 A

Chị học đến lớp 7 rồi h mới bt có cái quyển này e ạ
nên chị chịu k làm đc, không thì e chụp ảnh đăng lên học 24h ấy


TL:
32 : 7 = 4 ( dư 4 ) đây là cách làm của lớp 2 và 3
32 : 7 = \(\frac{32}{7}\)đây là cách làm của lớp 4
32 : 7 = 4,57 đây ;là cách làm của lớp 5
~HT~

1.a) \(125-25\cdot3\)= 125-75=50
b)\(125:5+75:5=25+15=40\)
c)\(30:3+7\cdot8=10+56=66\)
2.a)\(1-1+1-1=0\)
b)\(1+1-1-1=0\)
c)\(1-1-1+1=0\)
d)
3. Số học sinh trong mỗi tổ:
40:4=10( học sinh)
Số học sinh trong mỗi nhóm:
10:2=5( học sinh)
Đáp số: 5 học sinh
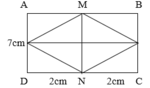
4, Hình vẽ trên có 3 hình chữ nhật là AGEB; BEDC; AGDC
Chu vi của hình chữ nhật AGEB là: (1+5)*2=12(cm)
Chu vi hình chữ nhật BEDC là: (2+5)*2=14(cm)
Chu vi hình chũa nhật AGDC là: 12+14=26(cm)
5. a)25dm c)205cm e)2005mm b)2500m d)2050m g)2050m

Đây là định lí đáng đồng ý với nhưng chưa được chứng minh chắc chắn. Định lí này được gọi là định lí Goldbach mở rộng (hay đôi khi cũng gọi là tổng ba số nguyên tố).
Đây là một trong những bài toán nổi tiếng của toán học và đã được các nhà toán học khám phá từ lâu. Mặc dù chưa có chứng minh chắc chắn cho định lí này đối với tất cả các số nguyên lớn hơn 2, nhưng các nhà toán học đã chứng minh rằng định lí Goldbach đúng đối với các số nguyên lớn hơn một số rất lớn. Ví dụ, đã chứng minh rằng mọi số chẵn lớn hơn 2 đều là tổng của hai số nguyên tố.
Trong những năm gần đây, các nhà toán học đã tiến bộ rất nhiều trong việc giải quyết định lí Goldbach. Năm 2012, Terence Tao chứng minh rằng mọi số lớn hơn hoặc bằng 10^14 đều là tổng của ba số nguyên tố và năm 2013, Yitang Zhang chứng minh rằng có vô số số nguyên tố giá trị tuyệt đối của chúng chỉ bằng cách ước tính đủ tốt.
Tuy nhiên, vẫn chưa có chứng minh chính xác cho định lí Goldbach đối với tất cả các số nguyên, và nó vẫn được coi là một trong những vấn đề toán học lớn nhất chưa được giải quyết.


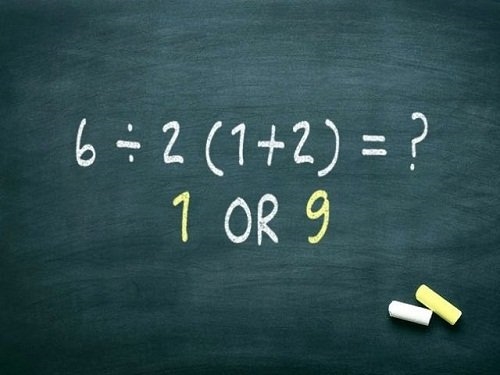


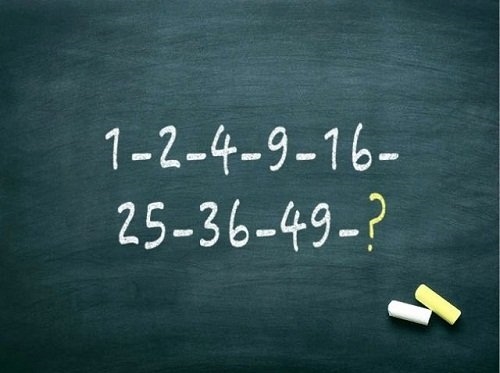




Đáp án là C