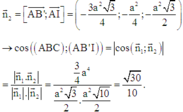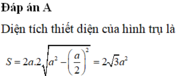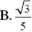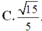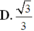Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác định thiết diện của hình chóp,hình lăng trụ dựa trên quan hệ vuông góc thường dựa trên các nguyên tắc sau: *Mặt phẳng chứa thiết diện qua một điểm và vuông góc với một đường thẳng thì chứa hai đường thẳng cắt nhau vuông góc với đường thẳng đó. * Mặt phẳng chứa thiết diện qua một đường thẳng và vuông góc với một mặt phẳng thì chứa một đường thẳng vuông góc với mặt phẳng đó.

Đáp án D
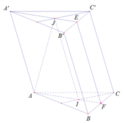
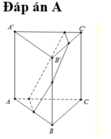
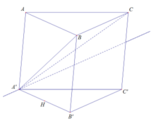
Gọi E và F lần lượt là trung điểm của B’C’ và BC
Xét (AIJ) và (ABC) có: F ∈ AI ⇒ F ∈ (AIJ) ⇒ (AIJ) ∩ (ABC) = AF
Xét ( AIJ) và (B’C’CB) có : F là điểm chung
IJ // (B’C’CB) ( I; J lần lượt là trọng tâm tam giác ABC và A’B’C’)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng a đi qua F và song song IJ
a cắt B’C’ tại E
⇒ (AIJ) ∩ (B’C’CB) = EF
Xét ( AIJ) và (A’B’C’) có:
E là điểm chung
AF // (A’B’C’)
⇒ giao tuyến 2 mặt phẳng là đường thẳng b đi qua E và song song AF
⇒ (AIJ) ∩ (A’B’C’) = A’E
Xét A’EFA có: AA’ // EF ( // IJ)
A’E // AF
A’EFA là hình bình hành

Để dựng thiết diện tạo bởi một mặt phẳng với hình chóp, hình hộp, hình lăng trụ, điều quan trọng là ta phải xác định các giao tuyến của mặt phẳng ấy với các mặt của hình chóp, hình hộp, hình lăng trụ
- Trước hết, ta cũng cần tìm giao điểm của các cạnh của hình chóp, hình hộp, hình lăng trụ
- Các đoạn thẳng nối các giao điểm ấy chính là các cạnh của thiết diện
- Ngoài ra cần sử dụng các kiến thức về quan hệ song song để giúp cho việc xác định các giao tuyến được chính xác và nhanh gọn.

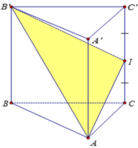
Đáp án B
Xét (A’B’C’) và (A’BC) có:
A’ là điểm chung
B’C’ // BC
giao tuyến của 2 mặt phẳng là đường thẳng d qua A’ song song với B’C’
⇒ d và B’C’ đồng phẳng
Mà d chứa A’
⇒ d thuộc mặt phẳng (A’B’C’)
Mà H ∈ A’B’ ⇒ H ∈ (A’B’C’)
⇒ Mặt phẳng đi qua d và H, cắt tứ diện ABC. A’B’C’ là (A’B’C’)

Đáp án A
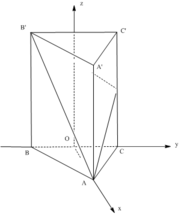
Gắn hệ trục tọa độ Oxyz như hình vẽ
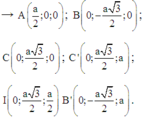
Vecto pháp tuyến của mặt phẳng
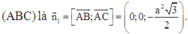
Vecto pháp tuyến của mặt phẳng (AB’I) là