Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : AB // CD ( gt )
\(OE\perp AB\)( gt )
\(\Rightarrow\)\(OE\perp CD\)
\(OG\perp CD\)( gt )
\(\Rightarrow\)OE trùng với OG nên ba điểm O ; E ; G thẳng hàng
AB và CD là các là đường phân giác các góc của hình thoi
OE = OF ( tính chất tia phân giác ) ( 1 )
OE = OH ( tính chất tia phân giác ) ( 2 )
OH = OG ( tính chất tia phân giác ) ( 3 )
Từ ( 1 ) ; ( 2 ) và ( 3 ) suy ra OE = OF = OH = OG
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên là hình chữ nhật
Ta có : AB // CD ( gt )
OE⊥AB( gt )
⇒OE⊥CD
OG⊥CD( gt )
⇒OE trùng với OG nên ba điểm O ; E ; G thẳng hàng
AB và CD là các là đường phân giác các góc của hình thoi
OE = OF ( tính chất tia phân giác ) ( 1 )
OE = OH ( tính chất tia phân giác ) ( 2 )
OH = OG ( tính chất tia phân giác ) ( 3 )
Từ ( 1 ) ; ( 2 ) và ( 3 ) suy ra OE = OF = OH = OG
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên là hình chữ nhật
chúc bn hok tốt @_@

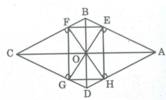
Ta có: AB // CD (gt)
OE ⊥ AB (gt)
⇒ OE ⊥CD
OG ⊥CD(gt)
Suy ra OE trùng với OG nên ba điểm O,E,G thẳng hàng.
BC // AD (gt)
OF ⊥ BC (gt)
⇒ OF ⊥ AD
OH ⊥ AD (gt)
Suy ra OF trùng với OH nên ba điểm O,H,F thẳng hàng.
Vì AC và BD là đường phân giác các góc của hình thoi nên:
OE = OF ( t/chất tia phân giác) (1)
OE = OH ( t/chất tia phân giác) (2)
OH = OG ( t/chất tia phân giác) (3)
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.

ABCD là hình thoi
=>AC vuông góc với BD tại trung điểm của mỗi đường
=>AC\(\perp\)BD tại O và O là trung điểm chung của AC và BD
Ta có:ABCD là hình thoi
=>AB//CD và AD//BC và AB=BC=CD=DA
Xét ΔEBO vuông tại E và ΔGDO vuông tại G có
BO=DO
\(\widehat{EBO}=\widehat{GDO}\)
Do đó: ΔEBO=ΔGDO
=>EO=GO
Ta có: ΔEBO=ΔGDO
=>\(\widehat{EOB}=\widehat{GOD}\)
mà \(\widehat{GOD}+\widehat{GOB}=180^0\)(hai góc kề bù)
nên \(\widehat{EOB}+\widehat{GOB}=180^0\)
=>E,O,G thẳng hàng
mà OE=OG
nên O là trung điểm của EG
Xét ΔOHD vuông tại H và ΔOFB vuông tại F có
OD=OB
\(\widehat{ODH}=\widehat{OBF}\)(hai góc so le trong, AD//BC)
Do đó: ΔOHD=ΔOFB
=>OH=OF
Ta có; ΔOHD=ΔOFB
=>\(\widehat{HOD}=\widehat{FOB}\)
mà \(\widehat{FOB}+\widehat{FOD}=180^0\)
nên \(\widehat{HOD}+\widehat{FOD}=180^0\)
=>H,O,F thẳng hàng
mà OH=OF
nên O là trung điểm của HF
ABCD là hình thoi
=>AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}\)
Xét ΔAEO vuông tại E và ΔAHO vuông tại H có
AO chung
\(\widehat{EAO}=\widehat{HAO}\)
Do đó: ΔAOE=ΔAOH
=>OH=OE
mà \(OH=\dfrac{HF}{2};OE=\dfrac{EG}{2}\)
nên HF=EG
Xét tứ giác EFGH có
O là trung điểm chung của EF và GH
=>EFGH là hình bình hành
Hình bình hành EFGH có HF=EG
nên EFGH là hình chữ nhật

Bài 2:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật
