Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành

Vì ABCD là hbh nên => AB=DC, AD=BC
có M là tđ của AB, P là trung điểm của DC mà AB=DC=>MB=DP (1)
N là tđ của BC, Q là tđ của AD mà AD=BC=> QD=BN (2)
Có góc QDB=góc MBN (ABCD là hbh) (3)
(1),(2),(3)=> tam giác MPN=tam giác QDP=>QP=MN
tương tự, cm QM=PN=> tứ giác QMNP có QM=BN, QP=MN => Tứ giác MNPQ là hbh( có hai cặp cạnh đối bằng nhau)

Bài khá dài đó.
Sorry nhé mik mới lớp 6 ak nên ko bít, tha lỗi nha!
ý kiến gì thì nhắn tin cho mik mai 7g
pp, ngủ ngon!

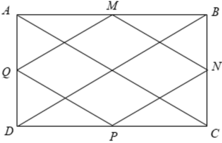
M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD
⇒ AM = MB; BN = NC; CP = DP; AQ = DQ
+ Xét Δ ABD có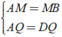
⇒ MQ là đường trung bình của Δ ABD.
⇒ QM = 1/2BD = 1/2AC ( 1 )
+ Xét Δ ABC có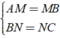
⇒ MN là đường trung bình của Δ ABC.
⇒ MN = 1/2BD = 1/2AC ( 2 )
+ Xét Δ BCD có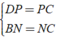
⇒ NP là đường trung bình của Δ BCD.
⇒ NP = 1/2BD = 1/2AC ( 3 )
+ Xét Δ ADC có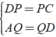
⇒ QP là đường trung bình của Δ ADC.
⇒ QP = 1/2BD = 1/2AC ( 4 )
Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.
⇒ MNPQ là hình thoi.

A B D C M N P Q Xét △ADC có:
AQ=QD và DP=PC
=>QP là đường trung bình=>QP//AC và QP=1/2 AC
Xét △ABC có:
AM=MB và BN=NC
=>MN là đường trung bình=>MN//AC và MN=1/2 AC
=>MN//QP và MN=QP
=>MNPQ là hbh
Xét △ABD có :
AQ=QD và MA=MB
=>QM là đường trung bình
=>QM=1/2 BD
Mà AC=BD (do ABCD là hcn)
=>QM=1/2 AC
=>QM=QP
=>MNPQ là h.thoi
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN=QP