Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ

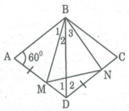
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều

Xét ΔABD có AB=AD và góc A=60 độ
=>ΔABD đều
=>góc ABD=góc ADB=60 độ và AB=AD=BD
Xét ΔBCD có CB=CD và góc C=60 độ
nên ΔBCD đều
=>BD=CB=CD và góc CBD=góc CDB=60 độ
Xét ΔBAM và ΔBDN có
BA=BD
góc BAM=góc BDN
AM=DN
=>ΔBAM=ΔBDN
=>BM=BN và góc ABM=góc DBN
=>góc DBN+góc DBM=60 độ
=>góc MBN=60 độ
=>ΔMBN đều
https://tailieumoi.vn/cau-hoi/hinh-thoi-abcd-co-goc-a-60-do-tren-canh-ad-lay-diem-m-tren-canh-137282.html
Nhắc lần thứ nhất, không copy câu trả lời từ nguồn khác.

tự vẽ hình nhé .
a) tứ giác ANMD có :
AN = 1/2 AB ; DM = 1/2 CD
\(\Rightarrow\)AN = DM (AB = CD )
mà AB // CD \(\Rightarrow\)AN // DM
\(\Rightarrow\)ANMD là hbh .
mà AN = AD ( = 1/2 AB ) \(\Rightarrow\)ANMD là hình thoi .
b) \(\Delta\)vuông AHB có :
HN là trung tuyến của AB . \(\Rightarrow\)HN = 1/2 AB
và MN = 1/2 AB ( MN = AN )
\(\Rightarrow\)\(\Delta\)HNM cân tại N .

Ta có : \(\widehat{BOM}\)+ \(\widehat{MON}\)+ \(\widehat{NOC}\)= \(180^0\) (kề bù)
\(\widehat{BOM}\)+ \(60^0\) + \(\widehat{NOC}\)= \(180^0\)
\(\widehat{BOM}\)+ \(\widehat{NOC}\) = \(120^0\) \(\left(1\right)\)
\(X\text{ét}\)\(\Delta NOC\)có :
\(\widehat{NOC}\)+ \(\widehat{ONC}\) + \(\widehat{NCO}\)= \(180^0\)
\(\widehat{NOC}\) + \(\widehat{ONC}\) + \(60^0\) = \(180^0\)
\(\widehat{NOC}\) + \(\widehat{ONC}\) = \(120^0\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)=) \(\widehat{BOM}\)= \(\widehat{ONC}\)
\(X\text{ét}\)\(\Delta OBM\)Và \(\Delta NCO\)có :
\(\widehat{MBO}\)= \(\widehat{OCN}\) ( cùng bằng 600 )
\(\widehat{BOM}\)= \(\widehat{ONC}\) ( chứng minh trên )
=) \(\Delta OBM\)đồng dạng với \(\Delta NCO\)( g-g )
Do \(\Delta OBM\) đồng dạng với \(\Delta NCO\)
=) \(\frac{BM}{CO}=\frac{OM}{ON}\)
Mà BO = OC
=) \(\frac{BM}{BO}=\frac{OM}{ON}\)
\(X\text{ét}\)\(\Delta OBM\) Và \(\Delta NOM\) có :
\(\frac{BM}{BO}=\frac{OM}{ON}\)
\(\widehat{B}\)\(=\)\(\widehat{MON}\) (cùng bằng \(60^0\))
=) \(\Delta OBM\)đồng dạng với \(\Delta NOM\) ( c - g - c )

