Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC

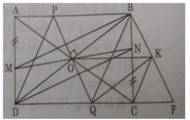
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.

a) Tự cm
b) Vì AB//DM mà ABvuoong góc với AC nên DM vuông góc với AC
Vì AH vuông góc với BC mà M thuộc BC nên CH vuông góc với AD
Xét tam giác ADC có:
DM vuông góc với AC
CM vuông góc với AD
mà DM cắt CM tại M
=> M là trực tâm của tam giác ADC
=> AM vuông góc với CD
=> đpcm
c) Xét tam giác NCm có
I là trung điểm của CM
=> IM=IN=IC
Xét tam giác IN< có
IM=IN
=> IMN cân tại I
=> IMN=INM góc
mà IMN=DMH
=> INM=DMH(3)
Xét tam giác AND có
H là trung điểm của AD
=> NH=HD=HA
tương tự tam giác NHD cân tại H
=>D=N( góc)(2)
mà HDN+DMH=90 độ(1)
Từ 1.2.3=> INM+MNH=90 độ
hay IN vuông góc với NH
đpcm