Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác AOD và tam giác BAD có:
{Dˆ:chungAOˆD=DAˆB=90{D^:chungAO^D=DA^B=90⇒ΔAOD≀ΔBAD(g.g)⇒ΔAOD≀ΔBAD(g.g)
b) Ta có: DAˆO=ABˆD=ABˆO(ΔAOD≀ΔBAD)DA^O=AB^D=AB^O(ΔAOD≀ΔBAD)
Và AOˆD=AOˆB=90AO^D=AO^B=90 (2 đường chéo vuông góc tại O)
Do đó ΔAOD≀ΔBOA(g.g)ΔAOD≀ΔBOA(g.g)
⇒ADAB=ODAO⇒ADAB=ODAO (1)
Lại có: {DAˆO:chungAOˆD=ADˆC=90{DA^O:chungAO^D=AD^C=90⇒ΔADC≀ΔAOD(g.g)⇒ΔADC≀ΔAOD(g.g)
⇒CDOD=ADAO⇔CDAD=ODAO⇒CDOD=ADAO⇔CDAD=ODAO (2)
Từ (1);(2)⇒ADAB=CDAD⇒AD2=AB⋅CD⇒ADAB=CDAD⇒AD2=AB⋅CD
c) Ta có: AB song song với DC (ABCD là hình thang)
⇒ABˆO=ODˆC(slt)⇒AB^O=OD^C(slt)
Và AOˆB=DOˆC(đ2)AO^B=DO^C(đ2)
Do đó ΔOCD≀ΔOAB(g.g)ΔOCD≀ΔOAB(g.g)
⇒k=OCOA=CDAB=94⇒k=OCOA=CDAB=94
⇒SΔOCDSΔOAB=k2=942=8116⇒SΔOCDSΔOAB=k2=942=8116
Vậy........................
Δ : tam giác. Chúc bạn học tốt nhé!

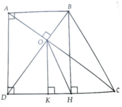
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

A B C D H O K G I M N P S T
a) Bạn xem lại đề nhé ! Mình vẽ hình và thấy không đúng.
b) Gọi M,N,P thứ tự là trung điểm các đoạn AD,BC,BD. Lúc này ta có:
MP là đường trung bình của \(\Delta\)BAD, PN là đường trung bình của \(\Delta\)CBD
Suy ra \(\frac{PM}{PN}=\frac{2AB}{2CD}=\frac{AB}{CD}\)(1) . Gọi S,T lần lượt là giao điểm của AH,CK với BD
Ta thấy \(\Delta\)OSH ~ \(\Delta\)ASB (g.g) => \(\frac{OH}{AB}=\frac{OS}{AS}\). Tương tự \(\frac{OK}{CD}=\frac{TO}{TC}\)
Mà \(\frac{OS}{AS}=\frac{TO}{TC}\)(Hệ quả ĐL Thales) nên \(\frac{OH}{OK}=\frac{AB}{CD}\) (2)
Từ (1) và (2) suy ra \(\frac{OH}{OK}=\frac{PM}{PN}\) hay \(\frac{OH}{PM}=\frac{OK}{PN}\)
Mặt khác ^MPN = ^MPB + ^BPN = ^BDC + ^BDA + ^BAD = ^BAD + ^ADC = ^HOK
Từ đó \(\Delta\)HOK ~ \(\Delta\)MPN (c.g.c) => ^OKH = ^PNM. Lại có KO vuông góc PN và CD
=> ^PNM và ^OKH phụ với góc hợp bởi OK và MN. Do vậy MN vuông góc với HK
Dễ thấy O,I,M và O,G,N thẳng hàng. Đồng thời \(\frac{OI}{IM}=\frac{OG}{GN}=2\)=> IG // MN (ĐL Thales đảo)
Như vậy IG vuông góc HK (đpcm).

a: Xét ΔABM vuông tại A và ΔDMC có
BA/DM=AM/CD
nên ΔABM đồng dạng với ΔDMC
b: Ta có: ΔABM đồng dạng với ΔDMC
nên góc AMB=góc DCM
=>góc AMB+góc DMC=góc DCM+góc DMC=90 độ
=>góc BMC=90 độ
=>ΔBMC vuông tại M
c: \(S=MB\cdot\dfrac{MC}{2}=10\cdot\dfrac{20}{2}=100\left(cm^2\right)\)