Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có m là trđ của cd rồi lại còn ef cắt bc tại m
a, xét tam giác DEM có AB // DM (gt) => ME/AE = DM/AB (ddl)
xét tam giác MFC có MC // AB (gt) => MF/FB = CM/AB (đl)
có DM = CM do M là trung điểm của CD (gt)
=> ME/AE = MF/FB xét tam giác ABM
=> EF // AB (đl)
b, gọi EF cắt AD;BC lần lượt tại P và Q
xét tam giác ABD có PE // AB => PE/AB = DE/DB (đl)
xét tam giác DEM có DM // AB => DE/DB = ME/MA (đl)
xét tam giác ABM có EF // AB => EF/AB = ME/MA (đl)
=> PE/AB = EF/AB
=> PE = EF
tương tự cm được FQ = EF
=> PE = EF = FQ
c, Xét tam giác DAB có PE // AB => PE/AB = DP/DA (đl)
xét tam giác ADM có PE // DM => PE/DM = AP/AD (đl)
=> PE/AB + PE/DM = DP/AD + AP/AD
=> PE(1/AB + 1/DM) = 1 (1)
xét tam giác AMB có EF // AB => EF/AB = MF/MB (đl)
xét tam giác BDM có EF // DM => EF/DM = BF/BM (đl)
=> EF/AB + EF/DM = MF/MB + BF/BM
=> EF(1/AB + 1/DM) = 1 (2)
xét tam giác ABC có FQ // AB => FQ/AB = CQ/BC (đl)
xét tam giác BMC có FQ // MC => FQ/MC = BQ/BC (đl)
=> FQ/AB + FQ/MC = CQ/BC + BQ/BC
có MC = DM (câu a)
=> FQ(1/AB + 1/DM) = 1 (3)
(1)(2)(3) => (1/AB + 1/DM)(PE + EF + FQ) = 3
=> PQ(1/AB + 1/DM) = 3
DM = 1/2 CD = 6
đến đây thay vào là ok

- Hình vẽ:
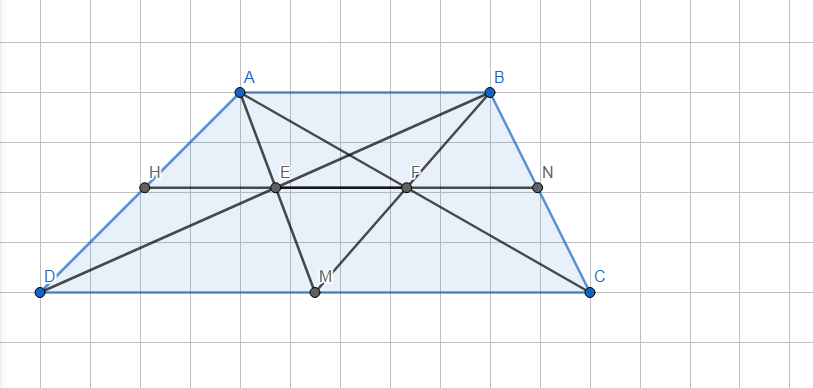
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).

A B C D M E F H N
a, MC // AB => MC/AB = MF/FB (hệ quả)
MB // AB => BM/AB = ME/EA (hệ quả)
Có BM = CM do M là trung điểm của BC (gt)
=> MF/FB = ME/EA
=> EF // AB
b, có HF // BM => AE/EM = HE/BM (hệ quả)
EF // MC => AE/EM = EF/MC (hệ quả)
BM = MC (Câu a)
=> HE = EF (1)
có EF // BM => EF/BM = BF/FM (hệ quả)
FN // MC => FN/MC = FB/FM (hệ quả)
BM = CM (Câu a)
=> EF = FN và (1)
=> HE = EF = FN

Bạn tự vẽ hình nha
a, Ta có : HE // DM => \(\frac{HE}{DM}=\frac{AE}{EM}\) ( 1 )
EF // MC => \(\frac{EF}{MC}=\frac{AE}{EM}\) ( 2 )
Từ ( 1 ) và ( 2 ) => \(\frac{HE}{DM}=\frac{EF}{MC}\)
Mà DM = MC => HE = EF ( * )
Ta có : EF // DM => \(\frac{EF}{DM}=\frac{BF}{FM}\) ( 3 )
FN // MC => \(\frac{FN}{MC}=\frac{BF}{FM}\) ( 4 )
Từ ( 3 ) và ( 4 ) => \(\frac{EF}{DM}=\frac{FN}{MC}\)
Mà DM = MC => EF = FN ( ** )
Từ ( * ) và ( ** ) => HE = EF = FN
b, Ta có : DM = MC = \(\frac{CD}{2}=\frac{12}{2}=6\left(cm\right)\)
Ta có : HE // AB => \(\frac{HE}{AB}=\frac{DH}{HA}\) ( 5 )
HE // DM => \(\frac{DM}{HE}=\frac{DH}{AH}\) ( 6 )
Từ ( 5 ) và ( 6 ) => \(\frac{HE}{AB}=\frac{DM}{HE}\)
=> HE2 = AB.DM = 7,5.6 = 45
=> HE = \(3\sqrt{5}\left(cm\right)\)
=> HN = HE + EF + FN
Mặt khác : HE = EF = FN
=> HN = 3.HE = \(3.3\sqrt{5}=9\sqrt{5}\left(cm\right)\)
