Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D C O / / // // a) Chứng minh \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD}\)
Ta có: \(\overrightarrow{AC}-\overrightarrow{CD}=\overrightarrow{AD}\left(đpcm\right)\) ( vì \(\overrightarrow{BA}=\overrightarrow{CD}\) )
b) Chứng minh \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=AC\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) ( theo quy tắc hình bình hành )
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC\left(đpcm\right)\)
bài này chả khó áp dụng 1 bước là ra ngay điều cần chứng minh rồi

Lời giải:
Vector cùng phương \(\overrightarrow{AB}\) và \(\overrightarrow{DC}\)
a)
- Áp dụng định lý Pitago:
\(AC=\sqrt{AD^2+DC^2}=\sqrt{10}a\) \(\Rightarrow |\overrightarrow{AC}|=\sqrt{10}a\)
\(BC=\sqrt{BM^2+MC^2}=\sqrt{AD^2+(DC-AB)^2}=\sqrt{2}a\)\(\Rightarrow |\overrightarrow{BC}|=\sqrt{2}a\)
- \(|\overrightarrow{BM}|=|\overrightarrow {AD}|=a\)
- Áp dụng định lý Pitago cho tam giác $ADM$:
\(AM=\sqrt{AD^2+DM^2}=\sqrt{AD^2+AB^2}=\sqrt{5}a\Rightarrow |\overrightarrow{AM}|=\sqrt{5}a\)
b)
Lấy \(T\) đối xứng với \(B\) qua \(M\). Khi đó \(AMTD,BDTC\) là hình bình hành. Theo quy tắc hình bình hành:
\(2\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AD}+(\overrightarrow{AD}+\overrightarrow{AB})=\overrightarrow{AD}+\overrightarrow{AM}=\overrightarrow{AT}\)
\(\overrightarrow{BD}+\overrightarrow{BC}=\overrightarrow{BT}\)

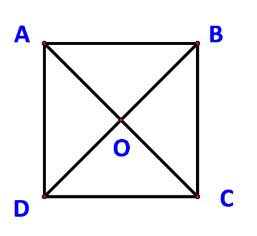
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \)
\( \Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)
b) Ta có: \(\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)
c) Ta có: \(\overrightarrow {DO} = \overrightarrow {OB} \)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA} \)
\( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)

hình bạn tự vẽ nha
ta có MN lần lượt là trung điểm của AD và BC
=> MN là đường tb trong ht ABCD
=>MN=\(\frac{AB+DC}{2}\)(1)=>2MN=AB+AC hay \(2\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{DC}\)
ta lại có\(\overrightarrow{BD}+\overrightarrow{CA}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{CD}+\overrightarrow{DA}=-\left(\overrightarrow{AB}+\overrightarrow{DC}\right)=-2\overrightarrow{MN}\)
khi đó \(\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}=\overrightarrow{MN}-2\overrightarrow{MN}=-\overrightarrow{MN}\) =>\(\left|\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}\right|=\left|-\overrightarrow{MN}\right|=MN\)
từ (1) =>MN=\(\frac{a+2a}{2}=\frac{3a}{2}\)