Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D H I J K
+) Ta có: \(\widehat{BAI}=\widehat{DAI}=\frac{1}{2}\widehat{BAD}\)( AI là phân giác \(\widehat{BAD}\))
\(\widehat{ADI}=\widehat{CDI}=\frac{1}{2}\widehat{ADC}\)(1)
=> \(\widehat{ADI}+\widehat{DAI}=\frac{1}{2}\widehat{ADC}+\frac{1}{2}\widehat{BAD}=\frac{1}{2}\left(\widehat{ADC}+\widehat{BAD}\right)=\frac{1}{2}.180^o=90^o\)
Xét \(\Delta\)AID có: \(\widehat{ADI}+\widehat{DAI}=90^o\)=> \(\widehat{AID}=90^o\)
=> \(\Delta\) AID vuông tại I; có H là trung điểm AD => \(HI=\frac{1}{2}AD=AI=ID\Rightarrow HI=\frac{10}{2}=5cm\)
Tương tự ta chứng minh được:
\(\Delta\)BJC vuông tại J; có K là trung điểm BC => \(JK=\frac{1}{2}AC=BK=KC\Rightarrow JK=\frac{12}{2}=6cm\)
+) Xét hình thang ABCD có: HK là đường trung bình
=> HK//DC (i)
và \(HK=\frac{1}{2}\left(AB+DC\right)=15\left(cm\right)\)
+) Xét tam giác HDI có HD=HI => Tam giác HDI cân tại H => ^HDI=^HDI (2)
Từ (1) , (2) => ^HID =^CDI mà hai góc ở vị trí so le trong => HI//DC (ii)
Tương tự chứng minh được KJ//DC (iii)
Từ (i); (ii); (iii) => H; I; J; K thẳng hàng => \(IJ=HK-HI-JK=15-5-6=4\left(cm\right)\)

Hình tự vẽ.
_________
Ta có:
AB//CD (GT) => AI ⊥ DI (phân giác của hai góc trong cùng phía bù nhau)
Gọi giao AB và DI là K.
Xét hai tam giác vuông AID và AIK có:
AI : cạnh chung, ^DAI = ^KAI (AI là phân giác)
Do đó: ΔAID = ΔAIK (cạnh góc vuông - góc nhọn kề)
=> DI = IK (hai cạnh tương ứng)
Mà DM = MA (M là trung điểm của DA)
=> MI là đường trung bình của ΔDAK => MI // AB (1)
AB//CD (GT) => BJ ⊥ CJ (phân giác của hai góc trong cùng phía bù nhau)
Gọi giao CJ và AB là H.
Xét hai tam giác vuông BJC và BJK có:
BJ : cạnh chung, ^CBJ = ^HBJ (BJ là phân giác)
Do đó: ΔBJC = ΔBJK (cạnh góc vuông - góc nhọn kề)
=> JC = JH (hai cạnh tương ứng)
Mà NC = NB (N là trung điểm của BC)
=> NJ là đường trung bình của ΔCBH => NJ // AB (2)
(1), (2) tương đương NJ và MI cùng nằm trên một đường thẳng song song với AB (tiên đề Ơ - clit)
Hay N, J, I, M thẳng hàng (đpcm)

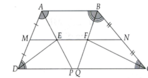
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 2B.
b) Ta có:
M N = 1 2 ( A B + C D ) = 1 2 ( a + c )
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.
Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ M F = 1 2 ( A B + D Q ) = 1 2 ( a + c − b )
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là F N = 1 2 C Q = 1 2 b .
Câu hỏi của :) - Toán lớp 8 - Học toán với OnlineMath