Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
giải dùm mình nha
A B C D A' C' B' E O F O'
Kí hiệu các điểm như hình vẽ.
Dễ dàng chứng minh được tam giác O'FO = tam giác O'C'C
=> OF = CC' (1) và OO' = O'C = 1/2OC => OO' = 1/3AO'
ta có OF là đường trung bình của tam giác BDB' vì \(\begin{cases}OB=OD\\FO\text{//}BB'\end{cases}\)
=> BB' = 2OF (2)
Từ (1) và (2) suy ra được BB'+CC' = 3OF (*)
Mặt khác, vì OF // AA' nên áp dụng định lí Talet ta có :
\(\frac{OF}{AA'}=\frac{OO'}{AO'}=\frac{1}{3}\Rightarrow AA'=3OF\) (**)
Từ (*) và (**) ta suy ra đpcm.
\(A=\left(2n-1\right)^3-2n+1\)
\(A=8n^3-6n+6n-1-2n+1\)
\(A=8n^3-2n=2n\left(4n^2-1\right)\)
\(A=2n\left(2n+1\right)\left(2n-1\right)\)
\(A=\left(2n-1\right)2n\left(2n+1\right)⋮6\) ( 3 số tự nhiên liên tiếp)
A B C D M E F G H N P Q I K
Gọi EFGH là tứ giác nội tiếp hình vuông
(\(E\in AB,F\in BC,G\in CD,H\in AD\)) , Từ E,F,G,H lần lượt dựng các đường thẳng vuông góc với BD tại P,Q,M,N; I và K là giao điểm của AG và EF.
Ta có : \(AI\ge AM=MP;GI\ge MP=GM;EK\ge EP=BP;KF\ge FQ=BK\)
\(\Rightarrow AG+EF=AI+IG+EK+KF\ge\left(PM+BQ\right)+\left(PN+BP\right)\)
Mặt khác, lại có : \(EH\ge NP;FG\ge MQ\)
\(\Rightarrow EF+FG+GH+HE\ge\left(PM+MQ+BQ\right)+\left(PN+NP+BP\right)\)
\(=BD+BD=2\)
\(\Rightarrow EF+FG+GH+GE\ge2\) (dpcm)
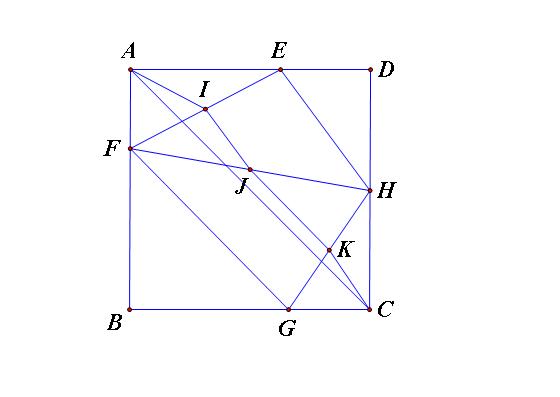
Ta có EF=2.AI,EH=2.IJ,GH=2.CK,EG=2.IK( Áp dụng tính chất đường trung bình và trung tuyến ứng với cạnh huyền trong tam giác vuông)
Suy ra \(P_{EFGH}=2\left(AI+IJ+JK+KC\right)\ge2AC=2\)
sách hay cái zì bạn?nếu đề thi hay bài tập bạn chụp rùi gửi mail(lethihuong34567890@gmail.com) cho mk đc hơm
? còn nếu sách thì chỉ cần chụp bìa dc gùi
\(\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow a^2c^2+a^2d^2+b^2c^2+b^2c^2+b^2d^2-ac^2-2abcd-b^2d^2-a^2d^2+2abcd-b^2c^2=0\)
=>dpcm
Tuyển " sư phụ "............................~~ K thành công !!! 
hình thang ABCD:M là trug điểmAD, N là trug điểmBC
ΔABD có: AM=MD(1),MI//AB(AB//MN)
từ (1) và (2)
Tương tự với ΔABC
Ta có: MI+IK+KN=MN
3+IK+3=11
VẬY MI=3cm, IK=5m,KN=3cm