Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),

Dựng hình bình hành \(ABEC\).
Khi đó \(E\in DC\).
Vì \(BD\perp AC\)mà \(AC//BE\)nên \(BE\perp BD\).
Kẻ \(BH\perp DE\).
Xét tam giác \(BED\)vuông tại \(B\)đường cao \(BH\):
\(\frac{1}{BH^2}=\frac{1}{BD^2}+\frac{1}{BE^2}\Leftrightarrow\frac{1}{4^2}=\frac{1}{5^2}+\frac{1}{BE^2}\Leftrightarrow BE=\frac{20}{3}\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.BD.BE=\frac{1}{2}.5.\frac{20}{3}=\frac{50}{3}\left(cm^2\right)\)

Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
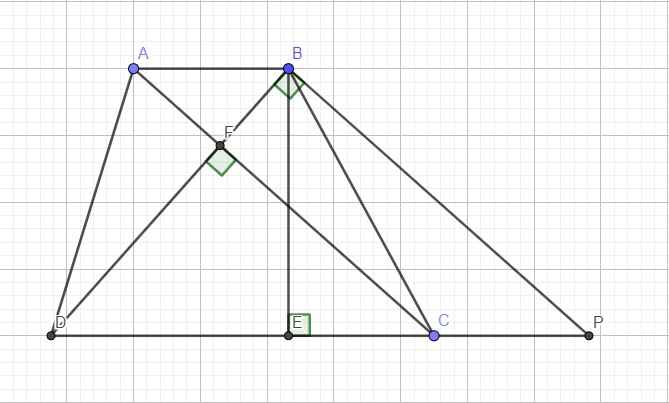
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)

chỉ cần kẻ đường thẳng // với AC cắt DC tại H rùi áp dụng hệ thức lượng vs py-ta-go là ra