Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé
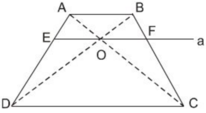
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF

Tam giác ABD có OE//AB
=>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB
=>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB
=>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3)
=> OE/AB = OF/AB
=> OE = OF (đpcm.)

Bài 1:
Áp dụng định lý Talet cho $EO\parallel DC$:
$\frac{OE}{DC}=\frac{AO}{AC}(1)$
Áp dụng định lý Talet cho $OF\parallel DC$:
$\frac{OF}{DC}=\frac{OB}{BD}(2)$
Áp dụng định lý Talet cho $AB\parallel CD$:
$\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow \frac{OA}{OA+OC}=\frac{OB}{OB+OD}\Leftrightarrow \frac{OA}{AC}=\frac{OB}{BD}(3)$
Từ $(1);(2);(3)\Rightarrow \frac{OE}{DC}=\frac{OF}{DC}$
$\Rightarrow OE=OF$ (đpcm)

A B C D E F O
a, xét tam giác ODC có : AB // DC
=> OA/OC = OB/OD = AB/DC (đl)
có : AB = 4; DC = 9 (gt)
=> OA/OC = OB/OD = 4/9
B, xét tam giác ABD có : EO // AB (gt) => EO/AB = DO/DB (hệ quả) (1)
xét tam giác ABC có FO // AB (gt) => OF/AB = CO/CA (hệ quả) (2)
xét tam giác ODC có AB // DC (gt) => DO/DB = CO/CA (hệ quả) (3)
(1)(2)(3) => OE/AB = OF/AB
=> OE = OF
xét tam giác ABD có : EO // AB(Gt) => EO/AB = DE/AD (hệ quả) (4)
xét tam giác ADC có EO // DC (gt) => OE/DC = EA/AD (hệ quả) (5)
(4)(5) => EO/AB + EO/DC = DE/AD + AE/AD
=> EO(1/AB + 1/DC) = 1 (*)
xét tam giác ACB có FO // AB (gt) => OF/AB = FC/BC (hệ quả) (6)
xét tam giác BDC có OF // DC (gt) => OF/DC = BF/BC (hệ quả) (7)
(6)(7) => OF/AB + OF/DC = FC/BC + BF/BC
=> OF(1/AB + 1/DC) = 1 (**)
(*)(**) => OF(1/AB + 1/DC) + OE(1/AB + 1/DC) = 1 + 1
=> (OE + OF)(1/AB + 1/DC) = 2
=> EF(1/AB + 1/DC) = 2
=> 1/AB + 1/DC = 2/EF

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF