Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).

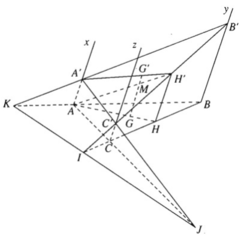
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
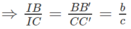
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
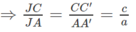
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
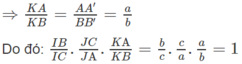
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
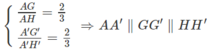
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
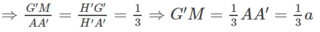
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
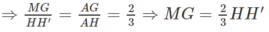
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
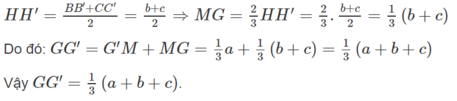

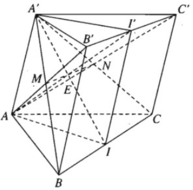
a) Ta có II′ // BB′ và II’ = BB’
Mặt khác AA′ // BB′ và AA’ = BB’ nên : AA′ // II′ và AA’ = II’
⇒ AA’II’ là hình bình hành.
⇒ AI // A′I′
b) Ta có:
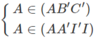
⇒ A ∈ (AB′C′) ∩ (AA′I′I)
Tương tự :
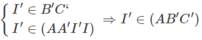
I′ ∈ (AB′C′) ∩ (AA′I′I) ⇒ (AB′C′) ∩ (AA′I′I) = AI′
Đặt AI′ ∩ A′I = E. Ta có:
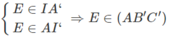
Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)
c) Ta có:
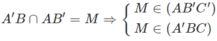
Tương tự:
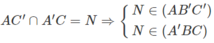
Vậy (AB′C′) ∩ (A′BC) = MN