Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có MN cắt BD tại M.
MN//CC', AC và A'D' chéo nhau.
b) MN ^ A'C' và B'D'
c) B'S' = 50cm, B'M = 5 41 c m
d) V =24000cm3

a) Diện tích đáy hình hộp chữ nhật:
\(AB.AC=10.20=200\left(cm^2\right)\)
Thể tích hình hộp chữ nhật:
\(V=S.h=200.15=3000\left(cm^3\right)\)
b) tam giác A'B'C' vuông tại B. Áp dụng định lý PITAGO ta có:
\(A'C'=\sqrt{A'B'^2+B'C'^2}=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
\(\Rightarrow AC'=\sqrt{AA'+A'C'^2}=\sqrt{15^2+10^2.5}=5\sqrt{29}\left(cm\right)\)


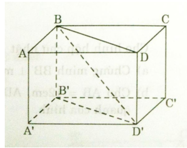
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)

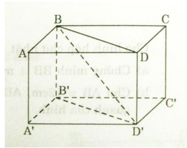
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)

a, Dễ CM AEOF là hình chữ nhật vì có 3 góc vuông
=>AO=EF
Mà AO=OC=AC/2 (O là tr.điểm AC do ABCD là hình chữ nhật)
=>EF=AC/2=12/2=6cm
b) CM \(\Delta AHO=\Delta CKO\left(ch-gn\right)\) => AH=KC
Mà AH//KC (cùng vuông góc với BD)
=>AHCK là hình bình hành => AK//HC
c, Có OA=OB=OC=OD (do ABCD là hình chữ nhật)
tam giác OAD cân có OE là đg cao nên cũng là trung tuyến => F là tr.điểm AD
Xét tam giác AHD vuông ở H có F là tr.điểm AD nên HF là trung tuyến ứng với cạnh huyền AD => HF=AF (=1/2AH)
Mà AF=OE (AEOF là hình chữ nhật)
=>HF=OE
Dễ CM EF là đg trung bình của tam giác ABD => EF//BD hay EF//OH=>EFHO là hình thang,mà HF=OE
=>EFHO là hình thang cân