Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

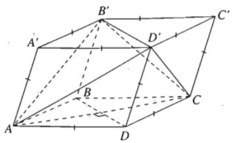
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên AC ⊥ BD
Theo tính chất của hình hộp: BD // B'D', do đó AC ⊥ B'D'.
Chứng minh tương tự ta được AB' ⊥ CD', AD' ⊥ CB'
Hai mặt phẳng (AA'C'C) và (BB'D'D) vuông góc với nhau khi hình hộp ABCD.A'B'C'D'là hình lập phương.

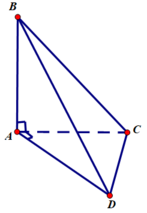
AB ⊥ AC, AB ⊥ AD nên AB ⊥ (AC, AD) hay AB ⊥ (ACD) (theo định lí trang 99)
AB ⊂ (ABC) nên (ABC) ⊥ (ACD) (theo định lí 1 trang 108)
AB ⊂ (ADB) nên (ADB) ⊥ (ACD)
AD ⊥ AC, AD ⊥ AB nên AD ⊥ (AC, AB) hay AD ⊥ (ABC)
AD ⊂ (ADB) nên (ADB) ⊥ (ABC)

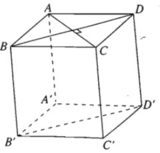
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD
Dễ thấy mặt chéo BDD'B' của hình hộp đã cho là hình bình hành, do đó BD // B′D′. Từ đó, theo bài 3.12 suy ra AC ⊥ B'D'.

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)


+) Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên tứ giác A'B'C'D'; ADD'A'; CC'D'D là hình thoi.
+) AB' // C'D và C'D \( \bot \) CD' nên AB' \( \bot \)CD'
+) AC // A'C' và A'C' \( \bot \) B'D' nên AC \( \bot \) B'D'
+) B'C // A'D và A'D \( \bot \) AD' nên B'C \( \bot \) AD'
Vậy ta đã chứng minh được rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.