Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

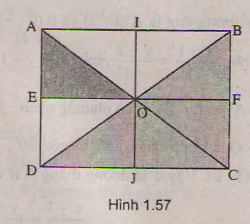
Phép đối xứng qua đường thẳng ***** biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
Phép đối xứng qua đường thẳng biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.

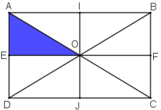
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
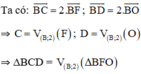
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.

Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng

Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
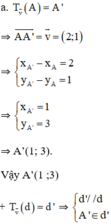
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :
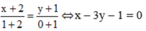

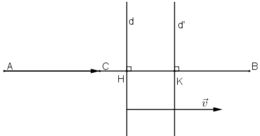
Lấy điểm A bất kì.
Gọi B = Đd (A) ; C = Đd’(B).
Gọi H, K là giao điểm của AB với d và d’ như hình vẽ.
Ta có:
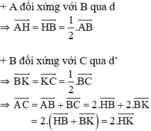
Mà d’ là ảnh của d qua phép tịnh tiến theo vectơ 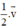
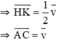
⇒ C là ảnh của A qua phép tịnh tiến theo vec tơ v→

a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vectơ v → = ( 2 ; 0 )
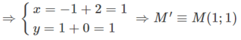
b) Gọi P(x;y) là ảnh của M(1;1) qua phép tịnh tiến theo v → = ( 2 ; 0 )
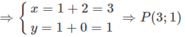
P(3;1) đối xứng qua trục Oy ta được M"(-3;1)

Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0
Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0

a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).