Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

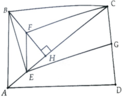
a) EF là đường trung bình của tam giác ABH => EF//AB; EF=1/2AB (1)
Có G là trung điểm của DC => GC//AB(DC//AB); GC=1/2AB(DC=AB) (2)
Từ (1)$(2) => EF//GC; EF=GC => Tứ giác EFCG là hình bình hành.
b) Xét tam giác EBH và tam giác CBH có:BH là cạnh chung
EHB=CHB=90 (gt)
EH=EC(H là trung điểm của EC)
Vậy tam giác EBH=tam giac CBH (cgv-cgv)
=>BEH=BCH ; EBH=CBH
Lại có:BEH+EBH+BCH+CBH=180 =>BEH=EBH=BCH=CBH=180/4=45 (3)
Co BCE+ECG=BCG
Ma BCG=90(ABCD là hcn); BCE=45(cmt)
=> ECG=45
Xét tam giác EGC có:EGC+GEC+ECG=180
=> EGC=180-(GEC+ECG)
=180-(90+45)=45 (4)
Tu (3)$(4) => BEG=90
c)Tu CM

Ta đi c/m ^BMK=90o
=================
Từ K, D hạ đường vuông góc KN, DP xuống AC
Xét tam giác BMK, ta có:
BK^2=BC^2+CK^2 = BC^2+CD^2/4 (1)
BM^2=BH^2+MH^2 = BH^2+ AH^2/4 (2)
MK^2=MN^2+NK^2=MN^2+BH^2/4 (3)
Ta có MN= MH-NH = AH/2-NH=AH/2-(CN-CH)=AH/2-AH/2+CH =CH (Do CN=CP/2=AH/2)
=>MN =CH, thay vào (3)
=> MK^2 = CH^2 +BH^2/4 (4)
Để c/m ^BMK=90o, ta c/m BK^2 =BM^2 +MK^2 (*)
Thay (1), (2), (4) vào (*), , ta được
BC^2+CD^2/4= BH^2+AH^2/4+CH^2+BH^2/4 (**)
Do BC^2= BH^2+CH^2
(**) => CD^2/4= AH^2/4+BH^2/4
=> CD^2=AH^2+BH^2
=> AB^2 = AH^2+BH^2 , đúng do tam giác AHB vuông tại H
Vậy ^BMK =90o

a, Chú ý EF là đường trung bình trong tam giác HAB
b, Chứng minh F là trực tâm tam giác BEC và sử dụng a)
c, Sử dụng tỉ số sinA trong tam giác vuông HAB và tỉ số tanA trong tam giác vuông BAC để tính AB, CB và AC, EC

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
b: Ta có: AEMFlà hình chữ nhật
=>AM cắt EF tại trung điểm của mỗi đường và AM=EF
=>O là trung điểm chung của AM và EF
K đối xứng M qua AC
=>AC vuông góc MK tại trung điểm của MK
ta có: AC\(\perp\)MK
AC\(\perp\)MF
MK,MF có điểm chung là M
Do đó: M,K,F thẳng hàng
=>F là trung điểm của MK
Xét ΔABC có MF//AB
nên \(\dfrac{MF}{AB}=\dfrac{CM}{CB}=\dfrac{1}{2}\)
mà \(\dfrac{MF}{MK}=\dfrac{1}{2}\)(F là trung điểm của MK)
nên \(MK=AB\)
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó: ABMK là hình bình hành
=>AM cắt BK tại trung điểm của mỗi đường
mà O là trung điểm của AM
nên O là trung điểm của BK
=>B,O,K thẳng hàng
c: Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có AC\(\perp\)MK
nên AMCK là hình thoi
=>AK//CM và CA là phân giác của góc KCM
=>AK//CB
Xét tứ giác ABCK có AK//BC
nên ABCK là hình thang
Để ABCK là hình thang cân thì \(\widehat{KCM}=\widehat{ABC}\)
=>\(\widehat{ABC}=2\cdot\widehat{ACB}\)
mà \(\widehat{ABC}+\widehat{ACB}=90^0\)
nên \(\widehat{ABC}=\dfrac{2}{3}\cdot90^0=60^0;\widehat{ACB}=90^0-60^0=30^0\)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên BC=2AM=10(cm)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(AC=10\cdot sin60=5\sqrt{3}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot5\sqrt{3}\cdot10\cdot sin30=5\cdot5\sqrt{3}\cdot\dfrac{1}{2}=\dfrac{25\sqrt{3}}{2}\left(cm^2\right)\)