Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

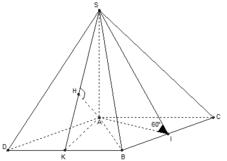
+) Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là:
(vì tam giác SIA vuông tại A nên góc SIA nhọn) ⇒ 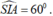
+) Xét tam giác SIA vuông tại A, 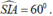
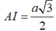 nên:
nên:
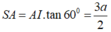
+) Dựng hình bình hành ACBD, tam giác ABC đều nên tam giác ABD đều.
+) Ta có:
AC // BD; BD ⊂ (SBD) nên AC // (SBD).
mà SB ⊂ (SBD) nên d(AC, SB) = d(A, (SBD)).
- Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ⊥ BD và 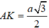 mà BD ⊥ SA nên BD ⊥ (SAK).
mà BD ⊥ SA nên BD ⊥ (SAK).
- Dựng AH ⊥ SK; H ∈ SK.
- Lại có AH ⊥ BD suy ra AH ⊥ (SBD).
- Vậy d(A, (SBD)) = AH.
- Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có:
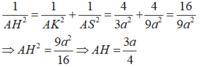
- Vậy d(AC, SB) = d(A, (SBD))
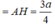

Gọi K là trung điểm của SA
=>KM//SC
=>SC//(KMB)
d(SC;BM)=d(S;(KBM))=SK/SA*d(A;(KBM))=d(A;(KBM))
=>ΔABC đều
=>BM vuông góc AC
=>BM vuông góc (SAC)
Kẻ AQ vuông góc KM
=>AQ vuông góc (KMB)
=>d(A;(KMB))=AQ
\(SC=\sqrt{9a^2+4a^2}=a\sqrt{13}\)
KM=1/2SC=a*căn 3/2
=>\(AQ=\dfrac{3\sqrt{13}}{13}\)
=>d(BM;SC)=3*căn 13/13

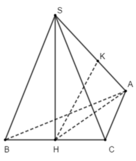
+ Gọi H là trung điểm của BC
Do tam giác ABC cân tại A nên AH ⊥ BC, tam giác SBC đều nên SH ⊥ BC
Mà (SBC) ⊥ (ABC)
Do đó SH ⊥ (ABC)
+ Gọi K là hình chiếu vuông góc của H lên SA ⇒ HK ⊥ SA
Ta có B C ⊥ S H B C ⊥ A H ⇒ B C ⊥ S A H ⇒ B C ⊥ H K
Vậy HK là đoạn vuông góc chung của BC và SA, do đó khoảng cách giữa BC và SA là HK.
+ Tính HK
Tam giác SBC đều cạnh a ⇒ SH = a 3 2
Tam giác ABC vuông cân tại A ⇒ AH = B C 2 = a 2
Tam giác SHA vuông tại H có HK là đường cao ⇒ 1 H K 2 = 1 S H 2 + 1 A H 2
HK = a 3 4
Vậy d(SA; BC) = a 3 4 .
Đáp án C

\(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(SAD\right)=SA\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
Gọi N là trung điểm BC \(\Rightarrow MN||AB\Rightarrow AB||\left(SMN\right)\)
\(\Rightarrow d\left(AB;SM\right)=d\left(AB;\left(SMN\right)\right)=d\left(A;\left(SMN\right)\right)\)
Từ A kẻ \(AH\perp SM\)
\(\left\{{}\begin{matrix}MN||AB\Rightarrow MN\perp AD\\SA\perp\left(ABCD\right)\Rightarrow SA\perp MN\end{matrix}\right.\) \(\Rightarrow MN\perp\left(SAD\right)\Rightarrow MN\perp AH\)
\(\Rightarrow AH\perp\left(SMN\right)\Rightarrow AH=d\left(A;\left(SMN\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow SA=\sqrt{SC^2-AC^2}=a\)
\(AM=\dfrac{AD}{2}=\dfrac{a}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=\dfrac{a\sqrt{5}}{5}\)

Đáp án D.
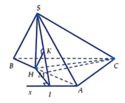
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
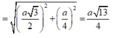
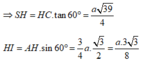
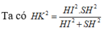
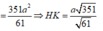
![]()
![]()

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)