Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai mặt phẳng (AB′D′)(AB′D′) và (A′C′D)(A′C′D) có giao tuyến là EFEF như hình vẽ.
Hai tam giác ΔA′C′D=ΔD′AB′ΔA′C′D=ΔD′AB′ và EFEF là đường trung bình của hai tam giác nên từ A′A′ và D′D′ ta kẻ 2 đoạn vuông góc lên giao tuyến EFEF sẽ là chung một điểm HH như hình vẽ.
Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng A′HA′H và D′HD′H.
Tam giác DEFDEF lần lượt có D′E=D′B′2=√132D′E=D′B′2=132, D′F=D′A2=52D′F=D′A2=52, EF=B′A2=√5EF=B′A2=5.
Theo hê rông ta có: SDEF=√614SDEF=614. Suy ra D′H=2SDEFEF=√30510D′H=2SDEFEF=30510.
Tam giác D′A′HD′A′H có: cosˆA′HD′=HA′2+HD′2−A′D′22HA′.HD′=−2961cosA′HD′^=HA′2+HD′2−A′D′22HA′.HD′=−2961.
Do đó ˆA′HD′≈118,4∘A′HD′^≈118,4∘ hay (ˆA′H,D′H)≈180∘−118,4∘=61,6∘(A′H,D′H^)≈180∘−118,4∘=61,6∘.
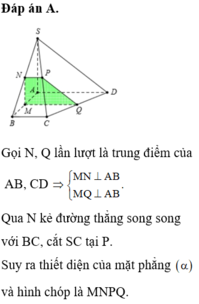
Gọi NN và PP lần lượt là trung điểm của SASA và ABAB.
Theo tính chất đường trung bình trong tam giác ta có NP // SBNP//SB và PC // AMPC//AM.
Suy ra \alpha = \widehat{NP, PC}α=NP,PC.
Ta có NP = \dfrac{SB}2 = \dfrac{\sqrt5}2NP=2SB=25 và PC = AM = \sqrt 5PC=AM=5;\\ NC = \sqrt{NA^2 + AC^2} = \sqrt{\dfrac14 + 8} = \dfrac{\sqrt{33}}2.NC=+=41=233.
\Rightarrow \cos \widehat{NPC} = \dfrac{NP^2+PC^2-NC^2}{2.NP.PC} = \dfrac{\dfrac54 + 5 - \dfrac{33}4}{2.\dfrac{\sqrt5}2.\sqrt5} = -\dfrac25⇒cosNPC=2.NP.PCNP2+PC2−NC2=2.25.545+5−433=−52.
Vậy \cos \alpha = \dfrac25cosα=52.2/5

Gặp những bài cần tính toán thế này làm biếng lắm, dựng hình thì dễ chứ tính thì chả muốn tính chút xíu nào.
Trong mp đáy, kéo dài AD và BC cắt nhau tại E \(\Rightarrow D\) là trung điểm AE (đường trung bình) \(\Rightarrow AE=AB=2a\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
\(\Rightarrow AD\in\left(\alpha\right)\)
Trong mp (SAB), kẻ \(AM\perp SB\Rightarrow M\in\left(\alpha\right)\)
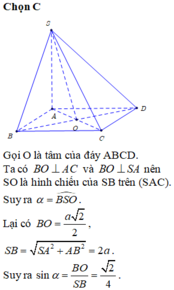
Dễ dàng chứng minh tam giác ACB vuông cân tại C (Pitago đảo) \(\Rightarrow BC\perp\left(SAC\right)\)
Trong mp (SAC), kẻ \(AN\perp SC\Rightarrow AN\perp\left(SBC\right)\Rightarrow AN\perp SB\Rightarrow N\in\left(\alpha\right)\)
\(\Rightarrow\) Thiết diện là tứ giác AMND
\(SB=SE=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(AM=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{AC^2+SA^2}=a\sqrt{3}\)
\(CN=\dfrac{AC^2}{SC}=\dfrac{2a\sqrt{3}}{3}\) ; \(EC=BC=a\sqrt{2}\Rightarrow EN=\sqrt{EC^2+CN^2}=\dfrac{a\sqrt{30}}{3}\)
\(DE=AD=a\)
\(S_{AME}=\dfrac{1}{2}AM.AE=...\)
\(S_{DNE}=\dfrac{1}{2}DE.EN.sin\widehat{DEN}=\dfrac{1}{2}DE.EN.\dfrac{AM}{\sqrt{AM^2+AE^2}}=...\)
\(\Rightarrow S_{AMND}=S_{AME}-S_{DNE}=...\)

Đáp án A
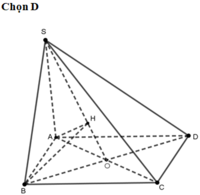
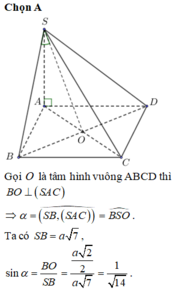
Ta có: B là hình chiếu của B lên (ABCD)
A là hình chiếu của S lên (ABCD)
Suy ra góc tạo bởi (ABCD) là góc φ = S B A ^ .
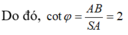






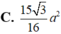

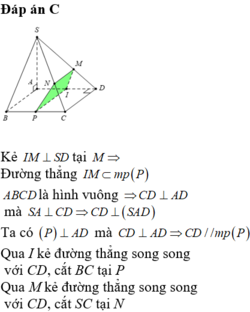

Bạn vẽ hình giúp mình nha ^^
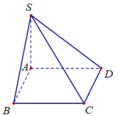
Xét (ABCD), kẻ \(MH\perp AB\left(H\in AB\right)\)
Xét (SAB), kẻ HF//SB(\(F\in SA\))
Có: \(\left\{{}\begin{matrix}MH\perp AB\\MH\perp SA\end{matrix}\right.\)\(\Rightarrow MH\perp\left(SAB\right)\)\(\Rightarrow MH\perp HF\)
Ta có: \(\alpha=\left(\stackrel\frown{SB,AM}\right)=\left(\stackrel\frown{HF,MH}\right)=arccos\left(\dfrac{HA}{HF}\right)\)
Xét \(\Delta AHF\) vuông tại A có: \(HF^2=HA^2+AF^2=a^2+\left(\dfrac{a}{2}\right)^2=\dfrac{5}{4}a^2\Rightarrow HF=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow\alpha=arccos\left(\dfrac{HA}{HF}\right)=arccos\left(\dfrac{2a}{a\sqrt{5}}\right)\approx26,57^o\) \(\Rightarrow cos\alpha=\dfrac{HA}{HF}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
là \(cos^{-1}\) trong máy tính á, đại loại kiểu ngược lại của cos... sin/cos/tan/sin sẽ đi với góc, còn arc + sin/cos/tan/cot là các cạnh ứng với công thức sin/cos/tan/cot