Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

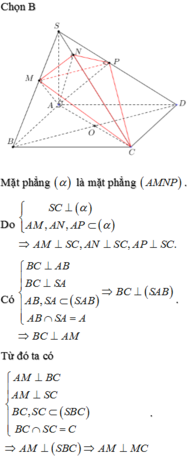
Chọn B.
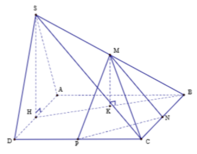
Gọi H là trung điểm của cạnh AD. Do tam giác SAD đều nên SH ⊥ AD
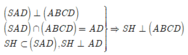
Gọi K là trung điểm của HB => MK//SH
Do đó: MK ⊥ ABCD => MK ⊥ (CNP).
Vậy MK là chiều cao của khối tứ diện CMNP.
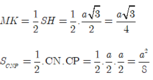
Thể tích khối tứ diện CMNP là
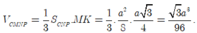

Gọi I là trung điểm AD \(\Rightarrow SI\perp AD\Rightarrow SI\left(ABCD\right)\Rightarrow d\left(I;\left(ABCD\right)\right)=SI\)
Ta có \(SM\cap\left(ABCD\right)=\left\{B\right\}\) và \(\frac{SB}{MB}=2\) nên \(d\left(M;\left(ABCD\right)\right)=\frac{1}{2}d\left(I;\left(ABCD\right)\right)=\frac{1}{2}SI=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\)
\(S_{CNP}=\frac{1}{2}\cdot CN\cdot CP=\frac{1}{2}\cdot\frac{1}{2}CD\cdot\frac{1}{2}\cdot BC=\frac{a^2}{8}\)
\(V_{M.CNP}=\frac{1}{3}\cdot d\left(M;\left(ABCD\right)\right)\cdot S_{CNP}=\frac{a^3\sqrt{3}}{96}\)


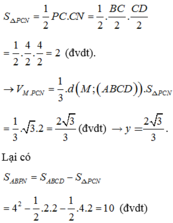


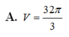
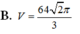
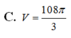
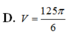


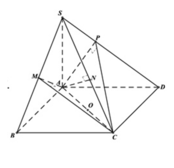


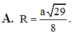

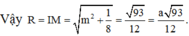
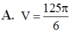
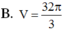
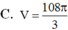
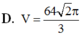

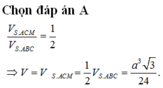
D H S M B N C K A P
Gọi H là trung điểm của AD. Do tam giác SAD là tam giác đều nên SH vuông góc với AD
Do mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) nên SH vuông góc với BP(1)
Xét hình vuông ABCD ta có :
\(\Delta CDH=\Delta BCP\Rightarrow CH\perp BP\) (2)
Từ (1) và (2) ta suy ra \(BP\perp\left(SHC\right)\)
Vì \(\begin{cases}MN||SC\\AN||CH\end{cases}\) \(\Rightarrow\left(AMN\right)||\left(SHC\right)\)
\(\Rightarrow BP\perp\left(AMN\right)\Rightarrow BP\perp AM\)
Kẻ vuông góc với mặt phẳng (ABCD), K thuộc vào mặt phẳng (ABCD), ta có :
\(V_{CMNP}=\frac{1}{3}MK.S_{CNP}\)
Vì \(MK=\frac{1}{2}SH=\frac{a\sqrt{3}}{4};S_{CNP}=\frac{1}{2}CN.CP=\frac{a^2}{8}\)
\(\Rightarrow V_{CMNP}=\frac{\sqrt{3}a^2}{96}\)