Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
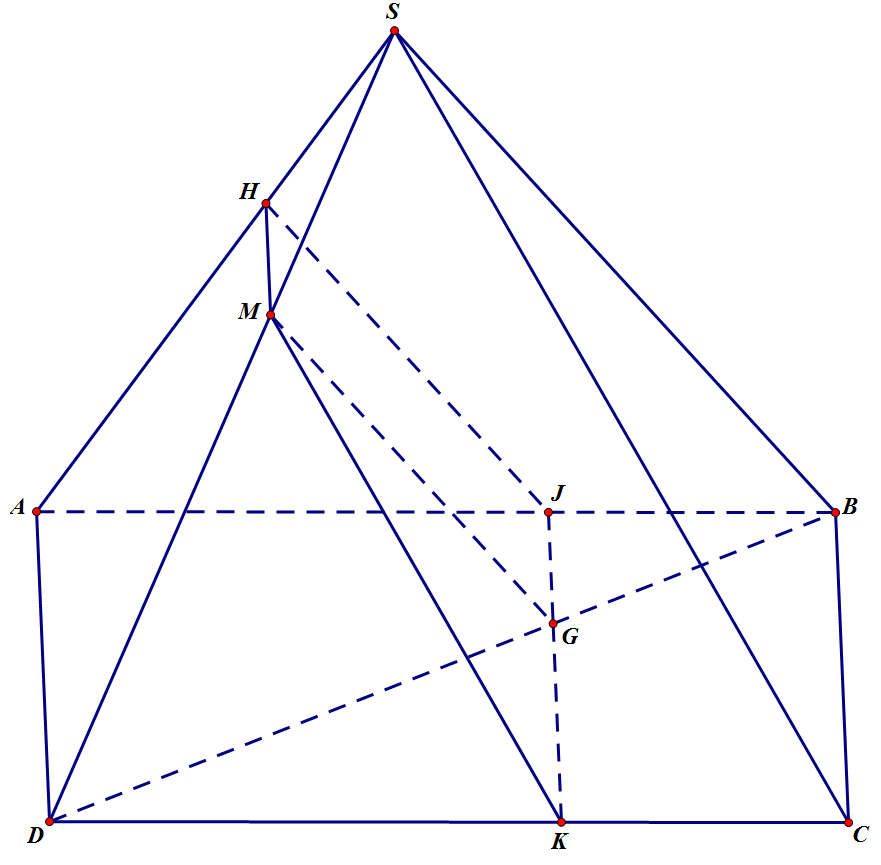
(α) và (SAD) cùng chứa điểm M. Mà (α) // AD nên (α) \(\cap\) (SAD) = d1 với d1 là đường thẳng đi qua M và song song với AD.
Trong (SAD) gọi H = d1 \(\cap\) SA ⇒ (SAD) \(\cap\) (α) = MH
(α) và (SBD) cùng chứa điểm M. Mà (α) // SB nên (α) \(\cap\) (SBD) = d2 với d2 là đường thẳng đi qua M và song song với SB.
Trong (SBD) gọi G = d2 \(\cap\) BD ⇒ (SAD) \(\cap\) (α) = MG
(SAB) và (α) cùng chứa điểm H. Mà (SAB) chứa SB, (α) chứa MG và ta lại có MG // SB
⇒ (SAB) \(\cap\) (α) = d3 với d3 là đường thẳng đi qua H và song song với SB và MG
Trong (SAB) gọi J = \(d_3\cap AB\) ⇒ (SAB) \(\cap\) (α) = HJ
Trong (ABCD) gọi K = JG \(\cap\) CD
Thiết diện cần tìm là tứ giác HMKJ (hình thang hai đáy HM, JK)
*Lưu ý : (α) không cắt (SBC) vì (α) // (SBC).
\(\cap\)
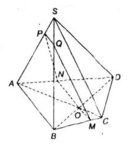
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.
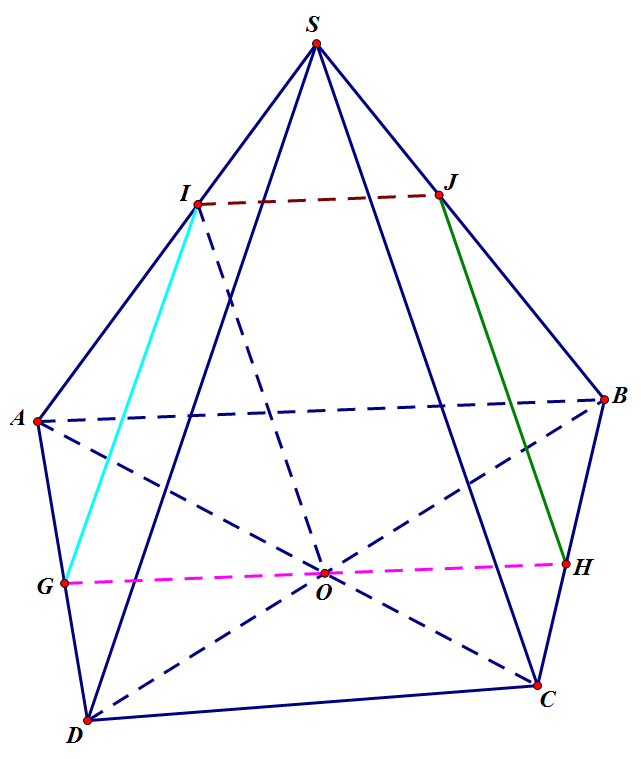
a, Giả thiết cho biết (α) và(ABCD) cùng chứa điểm O
Mà (α) // AB ⇒ (α) chứa đường thẳng song song với AB
⇒ (α) \(\cap\) (ABCD) = d1 . Với d1 là đường thẳng đi qua O và song song với AB. Trong (ABCD) gọi \(\left\{{}\begin{matrix}G=d_1\cap AD\\H=d_1\cap BC\end{matrix}\right.\)
⇒ (α) \(\cap\) (ABCD) = GH (hình vẽ)
Giả thiết cho biết :
Giả thiết cho biết (α) và (SAC) cùng chứa điểm O
Mà (α) // SC ⇒ (α) chứa đường thẳng song song với SC
⇒ (α) \(\cap\) (SAC) = d2 . Với d2 là đường thẳng đi qua O và song song với SC. Trong (SAC) gọi I = d2 \(\cap\) SA
⇒ (α) \(\cap\) (SAC) = O\(I\) (hình vẽ)
(P) và (SAB) cùng chứa điểm I. Mà (P) chứa GH, (SAB) chứa AB. Mà ta lại có AB // GH
⇒ (P) \(\cap\) (SAB) = d3. Với d3 là đường thẳng đi qua I và song song với AB và GH
Trong (SAB), gọi J = \(d_3\cap SB\)
⇒ Thiết diện cần tìm là tứ giác IJHG
Tứ giác này có IJ // HG nên nó là hình thang
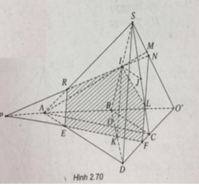
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
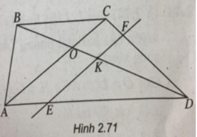
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do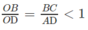 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.