Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
3: BC vuông góc SAB
=>AE vuông góc BC
mà AE vuông góc SB
nên AE vuông góc (SBC)
=>AE vuông góc SC
4: (SB;(SAC))=(SB;SD)=góc DSB
\(SD=\sqrt{SA^2+AD^2}=2a;SB=2a;DB=a\sqrt{2}\)
\(cosDSB=\dfrac{4a^2+4a^2-2a^2}{2\cdot2a\cdot2a}=\dfrac{3}{4}\)
=>góc DSB=41 độ

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ

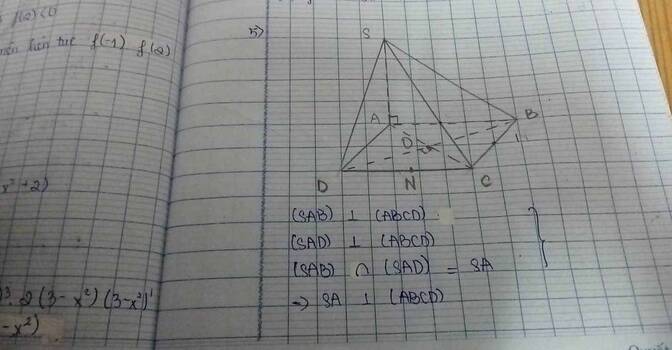
a: AD vuông góc SA
AD vuông góc AB
=>AD vuông góc (SAB)
AB vuông góc AD
AB vuông góc SA
=>AB vuông góc (SAD)
b:
\(SB=\sqrt{\left(3a\right)^2+a^2}=a\sqrt{10}\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{9a^2+2a^2}=a\sqrt{11}\)
\(SM=\dfrac{SA^2}{SB}=\dfrac{9a^2}{a\sqrt{10}}=\dfrac{9a}{\sqrt{10}}\)
\(cosMSC=cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{10a^2+11a^2-a^2}{2\cdot a\sqrt{10}\cdot a\sqrt{11}}=\dfrac{\sqrt{110}}{11}\)
vecto AM*vecto SC
=vecto SC*vecto SM-vecto SC*vecto SA
=\(SC\cdot SM\cdot cosCSM-SC\cdot SA\cdot cosASC\)
\(=a\sqrt{11}\cdot\dfrac{9}{\sqrt{10}}\cdot a\cdot\dfrac{\sqrt{110}}{11}-a\sqrt{11}\cdot3a\cdot\dfrac{3a}{a\sqrt{11}}=0\)
=>AM vuông góc SC

a: AD vuông góc SA
AD vuông góc AB
=>AD vuông góc (SAB)
AB vuông góc AD
AB vuông góc SA
=>AB vuông góc (SAD)
b:
\(SB=\sqrt{\left(3a\right)^2+a^2}=a\sqrt{10}\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{9a^2+2a^2}=a\sqrt{11}\)
\(SM=\dfrac{SA^2}{SB}=\dfrac{9a^2}{a\sqrt{10}}=\dfrac{9a}{\sqrt{10}}\)
\(cosMSC=cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{10a^2+11a^2-a^2}{2\cdot a\sqrt{10}\cdot a\sqrt{11}}=\dfrac{\sqrt{110}}{11}\)
vecto AM*vecto SC
=vecto SC*vecto SM-vecto SC*vecto SA
=\(SC\cdot SM\cdot cosCSM-SC\cdot SA\cdot cosASC\)
\(=a\sqrt{11}\cdot\dfrac{9}{\sqrt{10}}\cdot a\cdot\dfrac{\sqrt{110}}{11}-a\sqrt{11}\cdot3a\cdot\dfrac{3a}{a\sqrt{11}}=0\)
=>AM vuông góc SC

a: AD vuông góc SA
AD vuông góc AB
=>AD vuông góc (SAB)
AB vuông góc AD
AB vuông góc SA
=>AB vuông góc (SAD)
b:
\(SB=\sqrt{\left(3a\right)^2+a^2}=a\sqrt{10}\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{9a^2+2a^2}=a\sqrt{11}\)
\(SM=\dfrac{SA^2}{SB}=\dfrac{9a^2}{a\sqrt{10}}=\dfrac{9a}{\sqrt{10}}\)
\(cosMSC=cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{10a^2+11a^2-a^2}{2\cdot a\sqrt{10}\cdot a\sqrt{11}}=\dfrac{\sqrt{110}}{11}\)
vecto AM*vecto SC
=vecto SC*vecto SM-vecto SC*vecto SA
=\(SC\cdot SM\cdot cosCSM-SC\cdot SA\cdot cosASC\)
\(=a\sqrt{11}\cdot\dfrac{9}{\sqrt{10}}\cdot a\cdot\dfrac{\sqrt{110}}{11}-a\sqrt{11}\cdot3a\cdot\dfrac{3a}{a\sqrt{11}}=0\)
=>AM vuông góc SC

S A B C D H O K I L T
a) SA vuông góc với (ABCD) => SA vuông góc AD; hình thang ABCD vuông tại A => AD vuông góc AB
=> AD vuông góc (SAB), mà AD nằm trong (SAD) nên (SAB) vuông góc (SAD).
b) AD vuông góc (SAB), BC || AD => BC vuông góc (SAB) => B là hc vuông góc của C trên (SAB)
=> (SC,SAB) = ^CAB
\(SB=\sqrt{AS^2+AB^2}=\sqrt{2a^2+a^2}\)\(=a\sqrt{3}\)
\(\tan\widehat{CAB}=\frac{BC}{SB}=\frac{a}{a\sqrt{3}}=\frac{\sqrt{3}}{3}\)=> (SC,SAB) = ^CAB = 300.
c) T là trung điểm của AD, K thuộc ST sao cho AK vuông góc ST, BT cắt AC tại O, HK cắt AO tại I, AI cắt SC tại L.
BC vuông góc (SAB) => BC vuông góc AH, vì AH vuông góc SB nên AH vuông góc SC. Tương tự AK vuông góc SC
=> SC vuông góc (HAK) => SC vuông góc AI,AL. Lập luận tương tự thì AL,AI vuông góc (SCD).
Dễ thấy \(\Delta\)SAB = \(\Delta\)SAT, chúng có đường cao tương ứng AH và AK => \(\frac{HS}{HB}=\frac{KS}{KT}\)=> HK || BT || CD
=> d(H,SCD) = d(I,SCD) = IL (vì A,I,L vuông góc (SCD)) = \(\frac{IL}{AL}.AL=\frac{CO}{CA}.\frac{SI}{SO}.AL=\frac{1}{2}.\frac{SH}{SB}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}\)
\(=\frac{1}{2}.\frac{SA^2}{SA^2+SB^2}.\frac{AS.AC}{\sqrt{AS^2+AC^2}}=\frac{1}{2}.\frac{2a^2}{2a^2+a^2}.\frac{a\sqrt{2}.a\sqrt{2}}{\sqrt{2a^2+2a^2}}=\frac{a}{3}\)

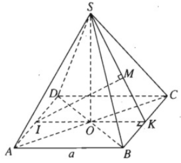
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 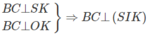
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 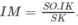
Ta lại có:
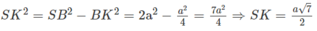
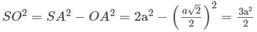
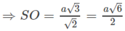
Do đó:
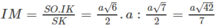
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 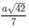



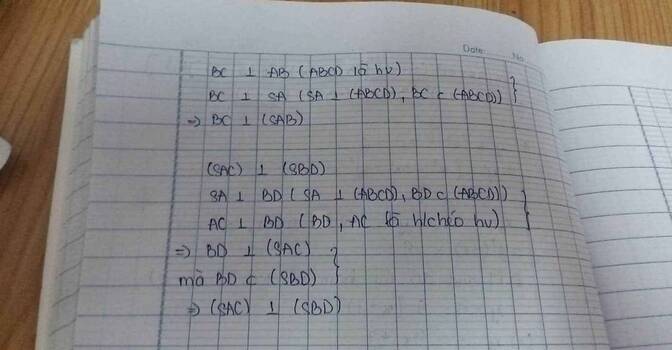
Tham khảo nhé!
https://hoc24.vn/cau-hoi/cho-hinh-chop-sabc-co-tam-giac-abc-vuong-tai-a-goc-abc60-sbaba-hai-mat-ben-sab-va-sbc-cung-vuong-goc-voi-mat-day-goi-hk-lan-luot-la.898787451803