Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Phạm Thùy Dương - Toán lớp 11 - Học toán với OnlineMath
Em tham khảo bài làm tại link này nhé!
Cộng đồng học tập online | Học trực tuyến
Lần sau các bài Toán lớp 10, 11, 12 các em đăng trong trang Cộng đồng học tập online | Học trực tuyến nhé! olm hầu như để giải đáp thắc mắc của HỌc sinh tiểu học và trung học em nhé :). Chúc em học tập tốt :)<3

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC

s A B C D a
1.SA \(\perp\)AB , SA\(\perp\)AD =>SAB vuông tại A, SAD vuông tại A
\(\begin{cases}AB\perp BC\left(hvABCD\right)\\SA\perp BC\left(SA\perp mpABCD\right)\end{cases}\) =>(SAB)\(\perp\)BC =>SB\(\perp\)BC =>SBC vuông tại B
\(\begin{cases}AD\perp CD\\SA\perp CD\end{cases}\) =>(SAD)\(\perp\)CD =>SD\(\perp\)CD =>SCD vuông tại D

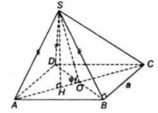
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
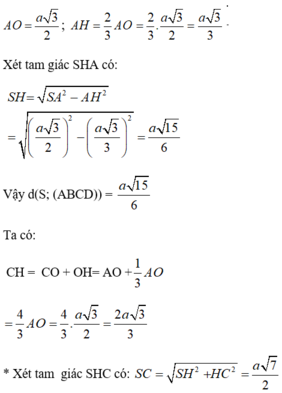


Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
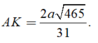

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
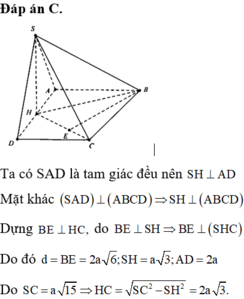
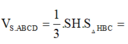
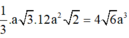
Trả lời:
Đáp án B
~Học tốt~
Dap an B
đúng hay ko mk ko chắc