Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (SAB) vuông góc (ABCD)
(SAB) giao (ABCD)=AB
SI vuông góc AB
=>SI vuông góc (ABCD)
b: CD vuông góc SI
CD vuông góc IK
=>CD vuông góc (SIK)
=>(SCD) vuông góc (SIK)

Do tam giác SAB cân và I là trung điểm AB \(\Rightarrow SI\perp AB\)
Mặt khác AB là giao tuyến của hai mặt phẳng vuông góc (SAB) và (ABCD)
\(\Rightarrow SI\perp\left(ABCD\right)\)
\(\Rightarrow SI\perp AD\) (1)
Lại có \(AD\perp AB\) (2) (giả thiết)
(1);(2)\(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
Theo cmt ta có \(\left\{{}\begin{matrix}SI\perp\left(ABCD\right)\\SI\in\left(SID\right)\end{matrix}\right.\) \(\Rightarrow\left(SID\right)\perp\left(ABCD\right)\)
c.
\(\overrightarrow{ID}.\overrightarrow{CK}=\left(\overrightarrow{IA}+\overrightarrow{AD}\right)\left(\overrightarrow{CD}+\overrightarrow{DK}\right)=\left(-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\right)\left(-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2+\dfrac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2\) (do AB vuông góc AD nên \(\overrightarrow{AB}.\overrightarrow{AD}=0\))
\(=0\) (ABCD là hình vuông nên AB=AD)
\(\Rightarrow ID\perp CK\)
Mà \(SI\perp\left(ABCD\right)\Rightarrow SI\perp CK\)
\(\Rightarrow CK\perp\left(SID\right)\)
\(\Rightarrow\left(SKC\right)\perp\left(SID\right)\)

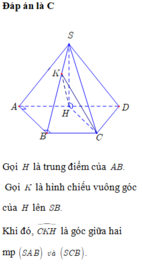
Đáp án A
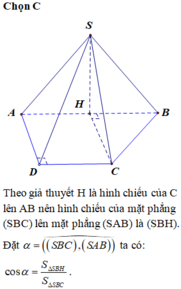
Gọi H là trung điểm của AB, tam giác SAB cân tại S do đó SH⊥AB mà (SAB)⊥ (ABCD) nên SH⊥ (ABCD). Góc giữa SC và đáy là SCH =600.
Tam giác BHC vuông tại B nên
![]()
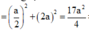
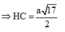
Tam giác SHC vuông tại H nên SH = SC.tanSCH ![]()
Do vậy 

Đáp án B.
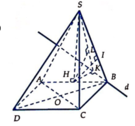
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
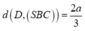
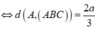
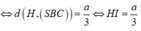
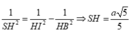
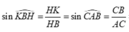
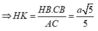
![]()
![]()
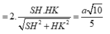
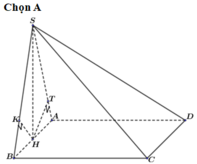

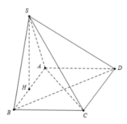


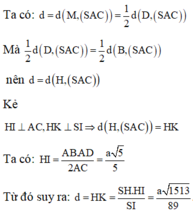

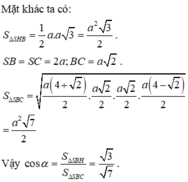
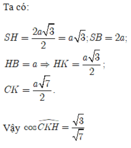
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)