Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ABCD là hình bình hành
=>AB//CD
b: SA cắt SC tại S
=>SA và SC là hai đường thẳng cắt nhau
c: SB cắt SD tại S
=>SB và SD là hai đường thẳng cắt nhau
d: \(SA\subset\left(SAB\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: SA và BC là hai đường thẳng chéo nhau
d: \(SD\subset\left(SCD\right)\)
\(AB\subset\left(ABCD\right)\)
Do đó: SD và AB là hai đường thẳng chéo nhau

a: ABCD là hình chữ nhật
=>AD//BC
b: SB cắt SC tại S
=>SB và SC là hai đường thẳng cắt nhau
c: SA cắt SD tại S
=>SA và SD là hai đường thẳng cắt nhau
d: \(SB\subset\left(SBC\right)\)
\(CD\subset\left(SCD\right)\)
Do đó: SB và CD là hai đường thẳng chéo nhau
e: \(SC\subset\left(SBC\right)\)
\(AD\subset\left(SAD\right)\)
Do đó: SC và AD là hai đường thẳng chéo nhau

a: Xét ΔSAC có M,N lần lượt là trung điểm của SA,SC
=>MN là đường trung bình của ΔSAC
=>MN//AC
mà MN không thuộc mp(ABCD) và \(AC\subset\left(ABCD\right)\)
nên MN//(ABCD)
b: \(A\in AN;A\in\left(ABD\right)\)
=>\(A\in AN\cap\left(ABD\right)\)
mà \(N\in SC\) không thuộc mp(ABD)
nên \(A=AN\cap\left(ABD\right)\)
c: \(S\in\left(SAC\right);E\in AC\subset\left(SAC\right)\)
Do đó: \(SE\subset\left(SAC\right)\)

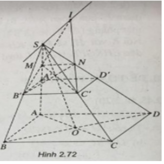
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).

a: BD cắt AC tại E
b: Xét ΔSAC có SM/SA=SN/SC
nên MN//AC
c: Trong mp(SAC), ta có: SE không song song với MN
=>SE cắt MN tại K
d: \(C\in SN\)
\(C\in\left(ABCD\right)\)
Do đó: \(SN\cap\left(ABCD\right)=C\)

a: 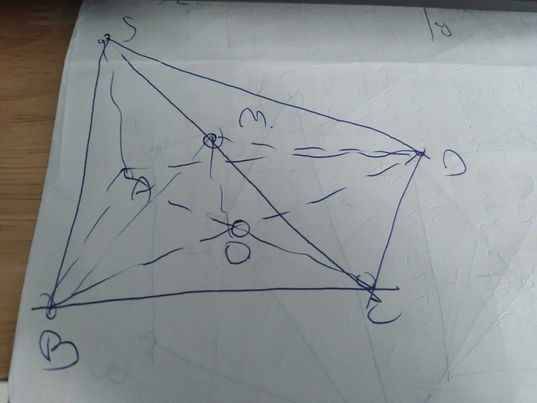
b: \(O\in AC\subset\left(SAC\right);M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔCAS có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình
=>OM//SA và OM=SA/2
OM//SA
\(SA\subset\left(SAD\right)\)
OM không nằm trong mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không nằm trong mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
OM//SA
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA
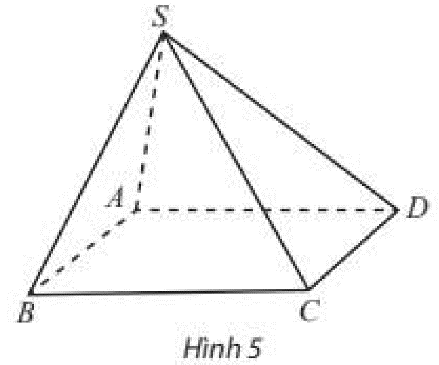
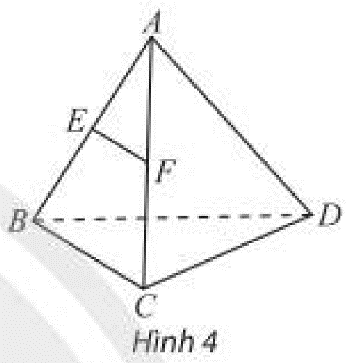

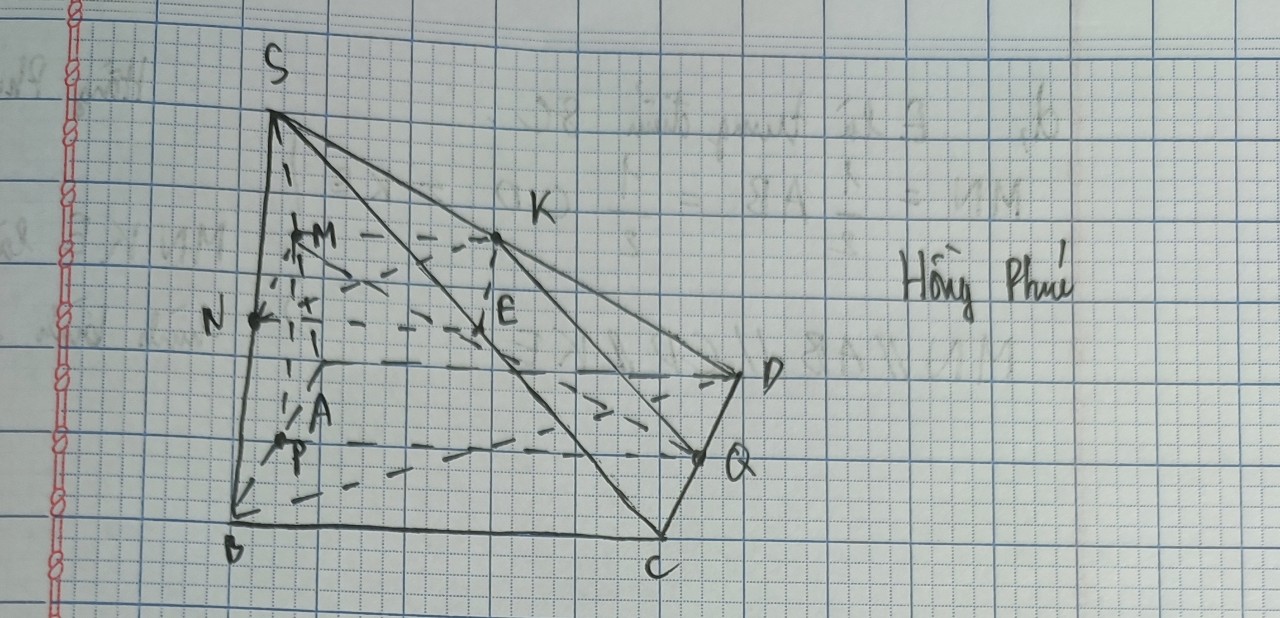
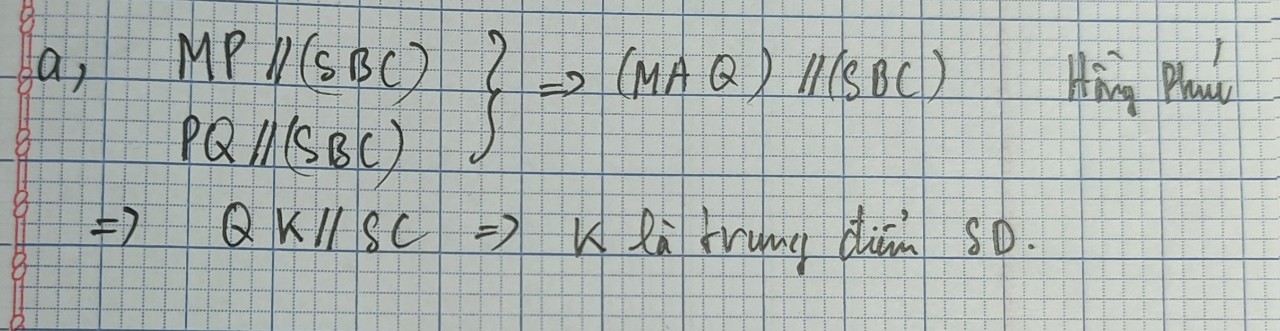

a, AB // CD
b, SA cắt SC tại S
c, SA và BC chéo nhau