Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D A B C N M I G H
\(d\left(M,BN\right)=\frac{\left|13\left(-1\right)-10.2+13\right|}{\sqrt{13^2+10^2}}=\frac{20}{\sqrt{269}}\)
\(H\in\Delta\Leftrightarrow H\left(3a;2a\right)\)
Gọi I là tâm ABCD, G là giao điểm của AC và BN. Ta thấy G là trọng tâm của tam giác BCD
Suy ra \(CG=\frac{2}{3}.CI=\frac{1}{3}AC\) mà \(AM=\frac{1}{4}AC\Rightarrow MG=\frac{5}{12}AC\Rightarrow CG=\frac{4}{5}MG\)
\(\Rightarrow d\left(C,BN\right)=\frac{4}{5}d\left(M,BN\right)=\frac{16}{\sqrt{269}}\Rightarrow d\left(H,BN\right)=2d\left(C,BN\right)=\frac{32}{\sqrt{269}}\)
\(\Leftrightarrow\frac{\left|13.3a-10.2a+13\right|}{\sqrt{269}}=\frac{32}{\sqrt{269}}\Leftrightarrow a=1\) hoặc \(a=\frac{-45}{19}\)
Vì H và M nằm khác phía đối với đường thẳng BN nên \(H\left(3;2\right)\)
Tiếp.........
Ta thấy \(CM=\frac{3AC}{4}=\frac{2AB}{4}=\frac{2CD}{4}=\frac{CD}{2}=CD=CH\Rightarrow\Delta MHN\) vuông tại M
HM có phương trình \(y-2=0\Rightarrow MN:x+1=0\Rightarrow N\left(-1;0\right)\Rightarrow C\left(1;1\right),D\left(-3;-1\right)\)
Do \(\overrightarrow{CM}=3\overrightarrow{MA}\Rightarrow A\left(\frac{-5}{3};\frac{7}{3}\right)\Rightarrow I\left(\frac{-1}{3};\frac{5}{3}\right)\Rightarrow B\left(\frac{7}{3};\frac{13}{3}\right)\)
Vậy \(A\left(\frac{-5}{3};\frac{7}{3}\right);B\left(\frac{7}{3};\frac{13}{3}\right);C\left(1;1\right);D\left(-3.-1\right)\)

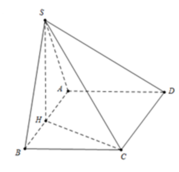
S B M H A E N C D
Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??


\(V_{ABSI}=V_{S.ABI}=\dfrac{1}{2}V_{S.ABCD}=\dfrac{a^3}{9}\)

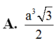

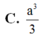
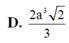
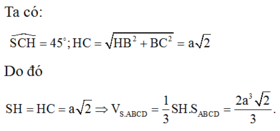
Ace Legona ngonhuminh giúp với