Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối BC và AD kéo dài cắt nhau tại F
\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối CM kéo dài cắt SD tại G
\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối SM kéo dài cắt CD tại E
\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)
Trong mp (ABCD), nối BE cắt AC tại H
\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)

a: \(M\in BC\subset\left(SBC\right);M\in\left(SOM\right)\)
Do đó: \(M\in\left(SBC\right)\cap\left(SOM\right)\)
mà \(S\in\left(SBC\right)\cap\left(SOM\right)\)
nên (SBC) giao (SOM)=SM
b: \(N\in CD\subset\left(SCD\right);N\in\left(SAN\right)\)
Do đó: \(N\in\left(SCD\right)\cap\left(SAN\right)\)
mà \(S\in\left(SCD\right)\cap\left(SAN\right)\)
nên \(\left(SCD\right)\cap\left(SAN\right)=SN\)
c: \(M\in BC\subset\left(SBC\right);M\in\left(SAM\right)\)
Do đó: \(M\in\left(SBC\right)\cap\left(SAM\right)\)
mà S thuộc (SBC) giao (SAM)
nên (SBC) giao (SAM)=SM
d: Trong mp(ABCD), gọi E là giao của AM với BD
\(E\in AM\subset\left(SAM\right);E\in BD\subset\left(SBD\right)\)
Do đó: E thuộc (SAM) giao (SBD)
mà S thuộc (SAM) giao (SBD)
nên (SAM) giao (SBD)=SE
e: Gọi F là giao của AN với BD trong mp(ABCD)
\(F\in AN\subset\left(SAN\right);F\in BD\subset\left(SBD\right)\)
=>F thuộc (SAN) giao (SBD)
mà S thuộc (SAN) giao (SBD)
nên (SAN) giao (SBD)=SF
f: \(CD\subset\left(SCD\right);CD\subset\left(ABCD\right)\)
Do đó: (SCD) giao (ABCD)=CD

a: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
c: \(N\in SB\subset\left(SAB\right);N\in\left(NCD\right)\)
=>\(N\in\left(SAB\right)\cap\left(NCD\right)\)
Xét (SAB) và (NCD) có
\(N\in\left(SAB\right)\cap\left(NCD\right)\)
AB//CD
Do đó: (SAB) giao (NCD)=ab, ab đi qua N và ab//CD//AB

a: Gọi O là giao điểm của AC và BD trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
2: Trong mp(ABCD), gọi E là giao điểm của AD và BC
\(E\in AD\subset\left(SAD\right);E\in BC\subset\left(SBC\right)\)
Do đó: \(E\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SE\)
3: Xét (SBA) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD

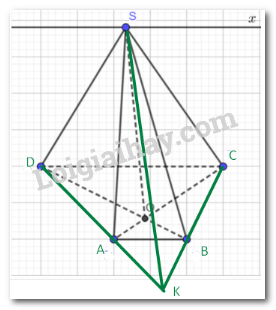
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).

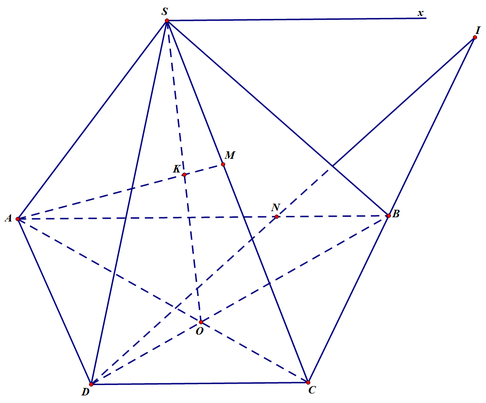
a, Gọi O là giao điểm của AC và BD
⇒ SO = (SAC) \(\cap\) (SBD)
b, (SAB) và (SCD) cùng đi qua điểm S và lần lượt chứa hai đường thẳng AB & CD, mà ta lại có AB // CD
⇒ (SAB) \(\cap\) (SCD) = Sx. trong đó Sx là đường thẳng đi qua S và song song với AB và CD
c, Trong (SAC) gọi K là giao điểm của SO và AM
⇒ AM \(\cap\) (SBD) = K
d, Trong (ABCD) gọi I = DN \(\cap\) BC
⇒ DN \(\cap\) (SBC) = I

Gọi giao điểm của AC và BD là K
\(K\in AC\subset\left(SAC\right)\)
\(K\in BD\subset\left(SBD\right)\)
Do đó: \(K\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SK\)
Gọi giao điểm của AB và CD là H
\(H\in AB\subset\left(SAB\right)\)
\(H\in CD\subset\left(SCD\right)\)
Do đó: \(H\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SH\)
Gọi M là giao điểm của AD và BC
\(M\in AD\subset\left(SAD\right)\)
\(M\in BC\subset\left(SBC\right)\)
Do đó: \(M\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SM\)
\(P\in SD\subset\left(SCD\right)\)
\(P\in\left(PAB\right)\)
Do đó: \(P\in\left(SCD\right)\cap\left(PAB\right)\)(1)
\(H\in AB\subset\left(PAB\right);H\in CD\subset\left(SCD\right)\)
Do đó: \(H\in\left(PAB\right)\cap\left(SCD\right)\)(2)
Từ (1) và (2) suy ra \(\left(SCD\right)\cap\left(APB\right)=HP\)

a)
Ta có:
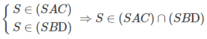
Giả sử:
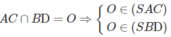
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
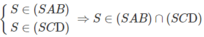
Ta lại có
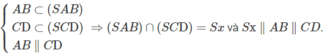
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.
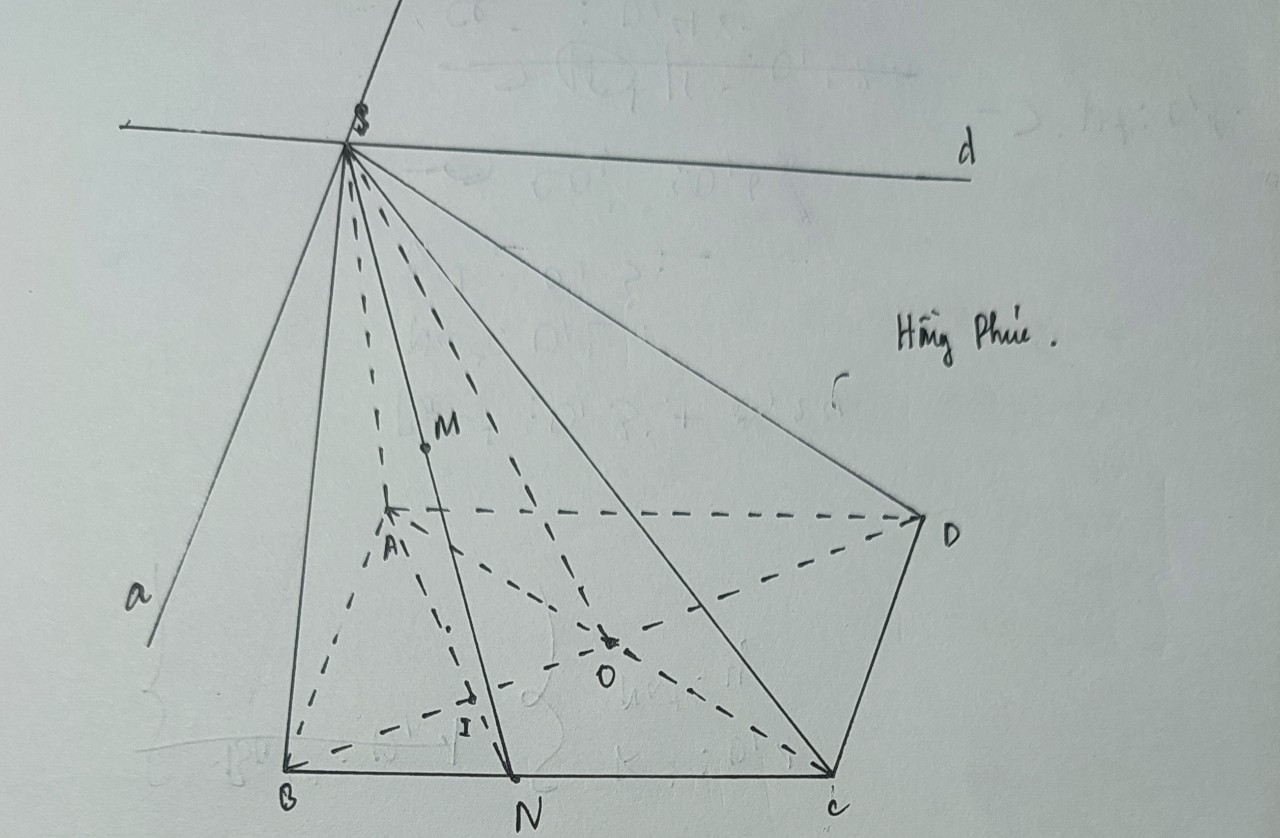

Giúp mình câu b, c với ạ
c: \(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
=>(SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
d: Gọi O là giao của BC và AD
\(O\in BC\subset\left(SBC\right);O\in AD\subset\left(SAD\right)\)
=>\(O\in\left(SBC\right)\cap\left(SAD\right)\)
=>\(\left(SBC\right)\cap\left(SAD\right)=SO\)