Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
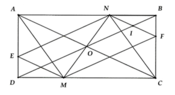
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

A B C D O M N P Q
a/
Ta có
MN//AB (gt)
AD//BC=> AM//BN
=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)
b/
Xét hbh ABCD
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét hbh APCQ có
IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> \(I\equiv O\) (đều là trung điểm AC) => M; N; I thẳng hàng
c/ Do \(I\equiv O\) (cmt) => AC; MN; PQ đồng quy tại O
Sử dụng định lý Menelaus. Nếu bạn chưa được học thì chứng minh nó như một bổ đề để sử dụng vào bài toán thôi.
Cho tam giác ABC. D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB . Khi đó, D, E, F thẳng hàng khi và chỉ khi \(\frac{AF}{BF}.\frac{BD}{CD}.\frac{CE}{AE}=1\)
CM phần thuận:
Kẻ các đường cao \(AA',BB',CC'\) xuống đường thẳng chứa \(D,E,F\)
Khi đó:
\(\frac{AF}{BF}=\frac{AA'}{BB'};\frac{BD}{CD}=\frac{BB'}{CC'}; \frac{CE}{AE}=\frac{CC'}{AA'}\)
\(\Rightarrow \frac{AF}{BF}.\frac{BD}{CD}.\frac{CE}{AE}=1\) (đpcm)
CM phần đảo:
Giả sử \(ED\cap AB\equiv F'\), do \(D,E,F'\) thẳng hàng nên theo kết quả cm ở phần thuận, ta có \(\frac{AF'}{BF'}.\frac{BD}{CD}.\frac{CE}{AE}=1\)
Kết hợp với \(\frac{AF}{BF}.\frac{BD}{CD}.\frac{CE}{AE}=1\Rightarrow \frac{AF}{BF}=\frac{AF'}{BF'}\)
Do đó, dễ dàng thấy \(F\equiv F'\Leftrightarrow D,E, F\) thẳng hàng.
Sử dụng kết quả trên vào bài toán:
Xét tam giác $MAS$ có: \(D\in MA, I\in SA, P\in MS\) và \(D,I,P\) thẳng hàng nên: \(\frac{DA}{DM}.\frac{IS}{IA}.\frac{PM}{PS}=1\)
\(\Leftrightarrow \frac{DA}{SQ}.\frac{IS}{IA}.\frac{AB}{PS}=1(*)\)
Xét tam giác $NAS$ có:
\(\frac{AB}{NB}.\frac{SI}{AI}.\frac{QN}{QS}=\frac{AB}{SP}.\frac{IS}{IA}.\frac{\\DA}{SQ1}=\) (theo \((*)\))
Do đó sử dụng kết quả bổ đề trên ta thu được \(B,I,Q\) thẳng hàng