Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

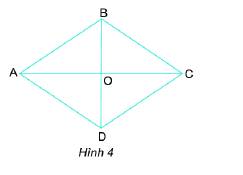
a) Các cạnh của hình thoi bằng nhau.
b) Kẻ đường thẳng qua B và vuông góc với BC. Đặt êke có góc vuông tại điểm cắt nhau giữa đường thẳng vừa kẻ và AD, đặt một cạnh góc vuông của êke trùng với đường thẳng ta thấy cạnh góc vuông còn lại của êke trùng khít với cạnh AD.
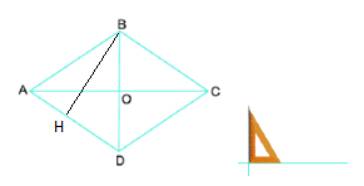
Khi đó BC và AD song song với nhau.
Tương tự AB và CD song song với nhau.
c) Tương tự như phần b, ta đặt đầu có góc vuông tại điểm O, đặt một cạnh góc vuông trùng với OB thì cạnh góc vuông còn lại trùng với OC hoặc OA. Khi đó AC và BD vuông góc với nhau.

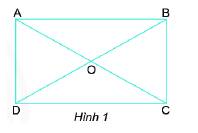
a) Các cạnh đối diện của hình chữ nhật bằng nhau (AB = CD = 4,5 cm, BC = AD = 2,5 cm).
Các góc của hình chữ nhật đều bằng nhau và bằng \( 90^0\)
b) AB và CD song song với nhau.
AD và BC song song với nhau.
c) AC và BD bằng nhau (cùng bằng 5,1 cm).

a) Hai cạnh bên BC = AD (=3 cm).
b) AB song song với CD.
c) AC = BD (=4,8 cm).

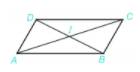
a)Xét 2 tam giác AOB và DOC
- BO=OD ( GT )
- AO=OC (gt)
- \(\widehat{AOB}=\widehat{DOC}\)(hai góc dối đỉnh)
=>tam giac AOB = tam giac DOC
b)Tự vẽ hình
Vì tam giác AOB=tam giác COD
\(\Rightarrow\)góc B=góc D(2 góc tương ứng)
Mà góc B và góc D ở vị trí SLT nên AB song song với CD

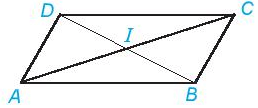
IA = IC và IB = ID => Điểm I là trung điểm của hai đường chéo AC và BD.

a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
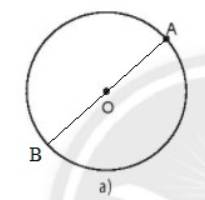
b) Độ dài IM = IM'.

Ta có: ABCD là hình bình hành
\(\left\{{}\begin{matrix}CD=AB=8cm\\BC=AD=5cm\end{matrix}\right.\)
Ta có: O là giao điểm 2 đường chéo
\(\Rightarrow AC=2OC=2.3=6\left(cm\right)\)
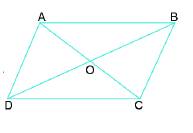
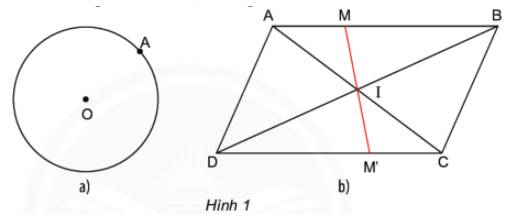
a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.