Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét tứ giác ABED có:
AB//DE;AB=DE
=>ABED là hình bình hành ( một cặp cạnh vừa song song vừa bằng nhau)
nên AD=BE
Xét tam giác EDA và tam giác ABE có:
AB=DE (gt)
AE là cạnh chung
AD=BE ( vừa chứng minh)
=>tam giác EDA =tam giác ABE
<=>tam giác EDA đồng dạng với tam giác ABE (1)
Xét tứ giác ABCE có:
AB//EC;AB=EC
=>ABCE là hình bình hành (một cặp cạnh vừa song song vừa bằng nhau
=>AE=BC
Xét tam giác ABE và tam giác CEB có:
AB=EC(gt)
BE là cạnh chung
AE=BC (vừa chứng minh)
=>tam giác ABE=tam giác CEB
<=>tam giác ABE đồng dạng với tam giác CEB (2)
từ (1) và (2)
=>tam giác EDA đồng dạng với tam giác ABE và đồng dang với tam giác CEB.
Ai biết cách vẽ kí hiệu đồng dạng không chỉ mình cách vẽ với cảm mơn bạn nhiều.
Vì ABCD là hình bình hành nên:
AB = CD (1)
Theo giả thiết:
AE = EB = 1/2 AB (2)
DF = FC = 1/2 CD (3)
Từ (1), (2) và (3) suy ra:
EB = DF và BE // DF.
Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
Suy ra: DE // BF
Ta có: ∠ (AED) = ∠ (ABF ) (đồng vị)
∠ (ABF) = ∠ (BFC) (so le trong)
Suy ra: ∠ (AED) = ∠ ( BFC)
Xét △ AED'và △ CFB ta có:
∠ (AED) = ∠ ( BFC) (chứng minh trên)
∠ A = ∠ C (tính chất hình bình hành)
Vậy: △ AED đồng dạng △ CFB (g.g)
Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
= 
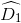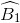(so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
Tham khảo thôi!
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
Giải:
∆ADC có OE // OC nên OEDC AEA
OEDC
OEDC = AEAD
∆BDC có OF // DC nên OFDCOFDC = BFBCBFBC
Mà AB // CD => AEADAEAD = BFBCBFBC(câu b bài 19)
Vậy OEDCOEDC = OFDCOFDC nên OE = OF.
