Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
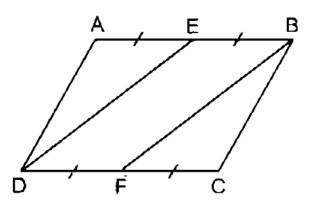
Ta có: AB = CD ( tính chất hình bình hành)
\(EB=\frac{1}{2}AB\left(gt\right)\)
\(FD=\frac{1}{2}CD\left(gt\right)\)
Suy ra: EB = FB (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
A B C D E F
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)

A B C D E F M N
Xét tam giác ADE và tam giác BCF có AD = BC (ABCD là hình bình hành)
Góc BAD = góc BCD , AE = CF = 1/2AB = 1/2CD
=> tam giác ADE = tam giác BCF (c.g.c)
=> góc AED = góc CFB . Mà AB // CD => góc CFB = góc ABF
=> góc AED = góc ABF mà hai góc này ở vị trí đồng vị
=> DE // BF
Xét tam giác MCD có NF // MD , DF = FC => NF là đường trung bình tam giác MCD
=> MN = NC (1)
Tương tự , ta cũng có ME là đường trung bình của tam giác ANB
=> AM = MN (2)
Từ (1) và (2) suy ra AM = MN = NC (đpcm)

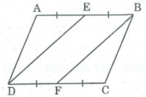
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy


Ta có \(EB=\dfrac{1}{2}AB\left(E.là.trung.điểm.AB\right)\)
\(FD=\dfrac{1}{2}CD\left(F.là.trung.điểm.CD\right)\)
\(AB=CD\left(hbh.ABCD\right)\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}CD\)
\(\Rightarrow BE=DF;BE//DF\left(AB//CD\right)\)
Do đó BEDF là hbg
\(\Rightarrow DE=BF\)

cậu tự vẽ hình nhé
ta có ABCD là hình bình hành => AB=CD =>BE=DF
và ta có AB//CD => BE//DF
=> EBCF là hình bình hành => DE=BF(ĐPCM)
ABCD là hình bình hành nên AB =CD (cạnh đối của hình bình hành) (1)
F là trung điểm của BC (theo đầu bài) nên BF = 1/2 BC (2).
E là trung điểm của AD (theo đầu bài) nên ED = 1/2 AD (3).
Từ (1), (2) và (3) suy ra BF = ED (4).
BF // ED (vì F nằm trên AB, E nằm trên AD; BC và AD là cạnh đối của hình bình hành ABCD nên BC//AD) (5).
Từ (4) và (5) suy ra BFDE là hình bình hành (2 cạnh đối song song và bằng nhau) =>BE = DF (điều phải chứng minh)