Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)\(VT=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{CO}+\overrightarrow{DO}+\overrightarrow{OC}+\overrightarrow{OC}=\overrightarrow{CO}+\overrightarrow{OC}+\overrightarrow{DO}+\overrightarrow{OD}=\overrightarrow{0}\)
2)\(VT=\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\)
3)\(VT=\overrightarrow{DO}+\overrightarrow{AO}=\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{AB}\)
4)\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\left(đpcm\right)=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD}=2\overrightarrow{MO}\left(đpcm\right)\)
Chúc bạn học tốt!!!!!
Đăng kí kênh Youtube 'Ban Mai Anime' giúp mình nhé!!!!

a) Chữa đề: \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(Ta\text{ }có:\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AB}\\ =\overrightarrow{CB}+\overrightarrow{DA}+\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=\overrightarrow{CB}+\overrightarrow{DA}\)
\(\)\(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CA}+\overrightarrow{CB}+\overrightarrow{DC}\\ =2\overrightarrow{CM}+2\overrightarrow{NC}=2\left(\overrightarrow{NC}+\overrightarrow{CM}\right)=2\overrightarrow{NM}\)
Vậy \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(\text{b) }\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{BC}=-\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{CA}+\overrightarrow{CB}\right)\\ =-\left[\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\right]\\ =-\left(2\overrightarrow{DM}+2\overrightarrow{CM}\right)=2\left(\overrightarrow{MD}+\overrightarrow{MC}\right)=4\left(\overrightarrow{MN}\right)\)
\(\text{c) }2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{DA}\right)+\left(\overrightarrow{AI}+\overrightarrow{NA}\right)\right]\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{DB}\right)+\overrightarrow{NI}\right]=2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)\)
Mà IN là dường trung bình \(\Delta BCD\)
\(\Rightarrow\left\{{}\begin{matrix}IN//BD\\IN=\frac{1}{2}BD\end{matrix}\right.\Rightarrow\overrightarrow{IN}=\frac{1}{2}\overrightarrow{BD}\\ \Rightarrow2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)=2\left(\overrightarrow{DB}+\frac{1}{2}\overrightarrow{DB}\right)=2\cdot\frac{3}{2}\overrightarrow{DB}=3\overrightarrow{DB}\)

TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).

1.D \(\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=\dfrac{1}{3}\left(2\overrightarrow{BM}\right)=\dfrac{2}{3}\overrightarrow{BM}=\overrightarrow{BG}\)
2.A \(\overrightarrow{DA}+\overrightarrow{DB}+2.\overrightarrow{DC}=2.\overrightarrow{DM}+2.\overrightarrow{DC}=0\)

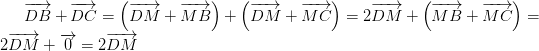
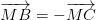
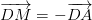
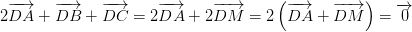
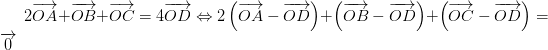
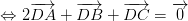 luôn đúng theo câu a
luôn đúng theo câu a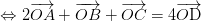 , với O là điểm tùy ý
, với O là điểm tùy ý
a) Ta có, theo quy tắc ba điểm của phép trừ:
Mặt khác,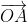 =
= 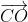 (2)
(2)
Từ (1) và (2) suy ra:
b) Ta có :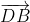 =
=  -
- 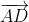 (1)
(1)
Từ (1) và (2) cho ta:
c) Ta có :
Từ (1), (2), (3) suy ra đpcm.
d)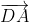 -
- 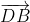 +
+ 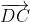 = (
= ( 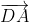 -
- 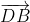 ) +
) + 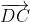 =
= 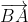 +
+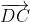 =
= 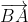 +
+  ( vì
( vì 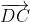 =
=  ) =
) =