Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AM}=\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}=-\overrightarrow{AM}+\overrightarrow{AB}\Rightarrow2\overrightarrow{AM}=\overrightarrow{AB}\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}=2\left(\overrightarrow{NA}+\overrightarrow{AD}\right)=-2\overrightarrow{AN}+2\overrightarrow{AD}\Rightarrow3\overrightarrow{AN}=2\overrightarrow{AD}\Rightarrow\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AD}\)
Do K là trung điểm MN
\(\Rightarrow\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
Theo tính chất hbh: \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
Do O là tâm hình bình hành \(\Rightarrow\overrightarrow{AO}=\overrightarrow{OC}=\dfrac{1}{2}\overrightarrow{AC}\)
Mà H là trung điểm OC \(\Rightarrow\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{OC}=\dfrac{1}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AH}=\overrightarrow{AO}+\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{KH}=\overrightarrow{KA}+\overrightarrow{AH}=-\overrightarrow{AK}+\overrightarrow{AH}\)
\(=-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}\)
=>A,N,D thẳng hàng và AN=2ND
ABCD là hình bình hành tâm O
=>O là trung điểm chung của AC và BD
H là trung điểm của OC
nên HO=HC=1/2CO
=>\(HO=HC=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot CA=\dfrac{1}{4}CA\)
\(\overrightarrow{AM}=\overrightarrow{MB}\)
=>AM=MB và M nằm giữa A và B
=>M là trung điểm của AB
AN+ND=AD
=>2ND+ND=AD
=>AD=3ND
=>AN/AD=2/3
=>\(\overrightarrow{AN}=\dfrac{2}{3}\cdot\overrightarrow{AD}\)
\(\overrightarrow{KH}=\overrightarrow{KM}+\overrightarrow{MH}\)
\(=\dfrac{1}{2}\overrightarrow{NM}+\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CH}\)
\(=\dfrac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{4}\left(\overrightarrow{CD}+\overrightarrow{CB}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)

Sai thì thôi nha :>
Theo đề ra: ABCD là hình bình hành
\(vectoAD+vectoAB=vectoAC\) và \(vectoAB+vectoAC=vectoBD\)
\(\Leftrightarrow vectoAD=-vectoAB+vectoAC\)
\(\Leftrightarrow vectoAD=vectoAB+vectoAC-2vectoAB=vectoBD-2vectoAB=b-2a\)
\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
suy ra \(2\overrightarrow{AD}=\overrightarrow{BD}+\overrightarrow{AC}\Leftrightarrow\overrightarrow{AD}=\frac{\overrightarrow{BD}+\overrightarrow{AC}}{2}=\frac{a+b}{2}\).

\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)

ABCD là hbh \(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\)
Ta có:
\(\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BD}\Rightarrow\overrightarrow{AD}-\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow2\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}=\dfrac{1}{2}\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{b}\)
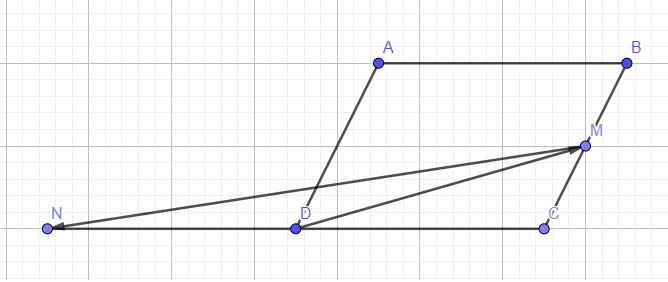
Gọi E là giao điểm của AC và BD
Hình vẽ:
\(\overrightarrow{MN}=\overrightarrow{DN}-\overrightarrow{DM}=\dfrac{2}{3}\overrightarrow{DB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(=\dfrac{4}{3}\overrightarrow{EB}+\dfrac{3}{4}\overrightarrow{BC}\)
\(=\dfrac{4}{3}\left(\overrightarrow{AB}-\overrightarrow{AE}\right)+\dfrac{3}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\dfrac{4}{3}\left(\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\right)+\dfrac{3}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\dfrac{7}{12}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{MC}=\overrightarrow{MD}+\overrightarrow{DC}=\dfrac{3}{4}\overrightarrow{AD}+\overrightarrow{AB}\)
\(=\dfrac{3}{4}\overrightarrow{BC}+\overrightarrow{AB}\)
\(=\dfrac{3}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)+\overrightarrow{AB}\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{MB}=\overrightarrow{AB}-\overrightarrow{AM}=\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(=\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{BC}\)
\(=\overrightarrow{AB}-\dfrac{1}{4}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\dfrac{5}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\)