Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì G là trọng tâm tam giác ABC nên \(GM = \dfrac{1}{3}AM\)
Kẻ \(BP \bot AM\) ta có
\(\begin{array}{l}{S_{GMP}} = \dfrac{1}{2}BP.GM\\{S_{ABM}} = \dfrac{1}{2}BP.AM\end{array}\)
\( \Rightarrow \dfrac{{{S_{GMP}}}}{{{S_{ABM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMP}} = \dfrac{1}{3}{S_{ABM}}\)(1)
Tương tự, kẻ \(CN \bot AM\), ta có
\(\begin{array}{l}{S_{GMC}} = \dfrac{1}{2}CN.GM\\{S_{ACM}} = \dfrac{1}{2}CN.AM\\ \Rightarrow \dfrac{{{S_{GMC}}}}{{{S_{ACM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)\end{array}\)
Cộng 2 vế của (1) và (2) ta có:
\(\begin{array}{l}{S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \Rightarrow {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\end{array}\)
b)
Ta có
\(\begin{array}{l}{S_{GAB}} = \dfrac{1}{2}BP.AG\\{S_{GAC}} = \dfrac{1}{2}CN.AG\end{array}\)
Xét \(\Delta BPM\) và \(\Delta CNM\) có:
\(\widehat {BPM} = \widehat {CNM} = {90^0}\)
BM = CM ( M là trung điểm của BC)
\(\widehat {PMB} = \widehat {CMN}\)(2 góc đối đỉnh)
\( \Rightarrow \Delta BPM = \Delta CNM\)(cạnh huyền – góc nhọn)
\( \Rightarrow \) BP = CN (cạnh tương ứng)
\( \Rightarrow {S_{GAB}} = {S_{GAC}}\)
Ta có: \(AG = \dfrac{2}{3}AM\)
\(\begin{array}{l}{S_{ACB}} = {S_{GAB}} + {S_{GAC}} + {S_{GCB}}\\ \Rightarrow {S_{ACB}} = {S_{GAB}} + {S_{GAC}} + \dfrac{1}{3}{S_{ABC}}\\ \Rightarrow \dfrac{2}{3}{S_{ABC}} = 2{S_{GAC}}\\ \Rightarrow \dfrac{1}{3}{S_{ABC}} = {S_{GAC}} = {S_{GAB}}\end{array}\)

Bài 2:
Ta có: AM=1/2BC
nên AM=BM=CM
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{B}\)
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{C}\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{MAB}+\widehat{B}+\widehat{MAC}+\widehat{C}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)=180^0\)
=>\(\widehat{BAC}=90^0\)
hay ΔABC vuông tại A

Ta có : AC//DB\(\Rightarrow S_{ABD}=S_{CDB}\left(1\right)\)
\(\Delta CDB=\Delta KAB\Rightarrow S_{CDB}=S_{KAB}\left(2\right)\)
AI//BK\(\Rightarrow S_{KAB}=S_{KIB}\left(3\right)\)
Từ (1),(2) và (3) suy ra \(S_{ABD}=S_{KIB}\Leftrightarrow S_{ABDE}=S_{BIJK}\left(4\right)\)
Với I,J là hình chiếu A xuống BC,HK
Tương tự ta cx có \(S_{ACFG}=S_{IJHC}\left(5\right)\)
Cộng (4) vfa (5) có ĐPCM
Từ đó suy ra Đ.L.Pitago

HÌnh bạn tự vẽ.
Bổ đề: (định lý Ptô-lê-mê)
Trong một tứ giác nội tiếp ABCD, ta có:
AC . BD = AB . CD + BC . AD
Áp dụng bổ đề trên cho tứ giác nội tiếp IPAN, ta có IA.NP = IP.AN + IN.AP = 2r(p - a) (ở đây ta đặt BC = a, CA = b, AB = c) và
\(p=\frac{a+b+c}{2}\) thì AN = AP = p - a.
Tương tự IB . PM = 2r(p - b)
IC . MN = 2r(p - c)
Nhân theo vế ba đẳng thức trên ta được:
\(IA.IB.IC.MN.NP.PM=8r^3\left(p-a\right)\left(p-b\right)\left(p-c\right)\).
Mặt khác, vì r là bán kính đường tròn ngoại tiếp \(\Delta MNP\)nên MN.NP.PM = \(4rS_{MNP}\).
Ngoài ra theo công thức Hê-rông ta có:
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\).Do đó:
IA . IB . IC. 4rSMNP = \(\frac{8r^3.S^2_{ABC}}{p}=8r^4S_{ABC}\)(vì SABC = pr), suy ra đpcm
P/s: Chỗ nào không hiểu thì bạn chỉ việc vẽ hình ra và quan sát hình là được :))

Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
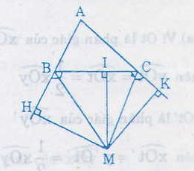
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc ˆBACBAC^
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)

Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của gócA

S1 = 5 => S2 = 3.5 + 1 = 16 => S3 = 16/2 = 8 => S4 = 8/2 = 4 => S5= 4/2 = 2 => S6 = 2/2 = 1
=> S7 = 4 => S8 = S5 = 2 => S9 = S6 = 1. Tiếp tục như vậy, ta thấy bộ 3 số 4; 2; 1 lặp lại trong dãy số
Vậy Từ S4 trở đi, cứ 3 số liên tiếp trong dãy bộ 3 số (4;2;1) sẽ lặp lại
Có thể viết dãy số trên như sau: (5;16;8) (4;2;1) (4;2;1) (4;2;1).....(4;2;1)
Có 2012 : 3 = 670 (dư 2) => đến S2012 có 670 bộ số, dư 2 số
=> S2012 là số thứ 2 trong bộ số thứ 671 => S2012 = 2


a: Kẻ CH vuông góc với AM
\(S_{AGC}=\dfrac{CH\cdot AG}{2}\)
\(S_{GMC}=\dfrac{CH\cdot MG}{2}\)
mà AG=2MG
nên \(S_{AGC}=2S_{GMC}\)
b: Kẻ GK vuông góc với BC
\(S_{GMB}=\dfrac{BM\cdot GK}{2}\)
\(S_{GMC}=\dfrac{MC\cdot GK}{2}\)
mà BM=CM
nên \(S_{GMB}=S_{GMC}\)