Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
A B C D H 1
a) Xét tam giác BDC vuông tại C có:
\(DC^2+BC^2=DB^2\)
\(\Rightarrow BD=\sqrt{DC^2+BC^2}\)( DC=AB)
\(\Rightarrow BD=10\left(cm\right)\)
b) tam giác BDA nhé
Xét tamg giác ADH và tam giác BDA có:
\(\hept{\begin{cases}\widehat{D1}chung\\\widehat{AHD}=\widehat{BAD}=90^0\end{cases}\Rightarrow\Delta ADH~\Delta BDA\left(g.g\right)}\)
c) Vì tam giác ADH đồng dạng với tam giác BDA (cmt)
\(\Rightarrow\frac{AD}{DH}=\frac{BD}{DA}\)( các cạnh t,.ứng tỉ lệ )
\(\Rightarrow AD^2=BD.DH\)
d) Xét tan giác AHB và tam giác BCD có:
\(\hept{\begin{cases}\widehat{AHB}=\widehat{BCD}=90^0\\\widehat{ABH}=\widehat{DBC}=45^0\end{cases}\Rightarrow\Delta AHB~\Delta BCD\left(g.g\right)}\)
( góc= 45 độ bạn tự cm nhé )
e) \(S_{ABD}=\frac{1}{2}AD.AB=\frac{1}{2}AH.BD\)
\(\Rightarrow AD.AB=AH.BD\)
\(\Rightarrow AH=4,8\left(cm\right)\)
Dùng Py-ta-go làm nốt tính DH
Bài 1
A B C H I D
a) Áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\)
Thay AB=3cm, AC=4cm
\(\Rightarrow3^2+4^2=BC^2\)
<=> 9+16=BC2
<=> 25=BC2
<=> BC=5cm (BC>0)

Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
Vì AD là pg \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Leftrightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{BC}{AC+AB}=\dfrac{10}{14}=\dfrac{5}{7}\Rightarrow DC=\dfrac{30}{7}cm;BD=\dfrac{40}{7}cm\)
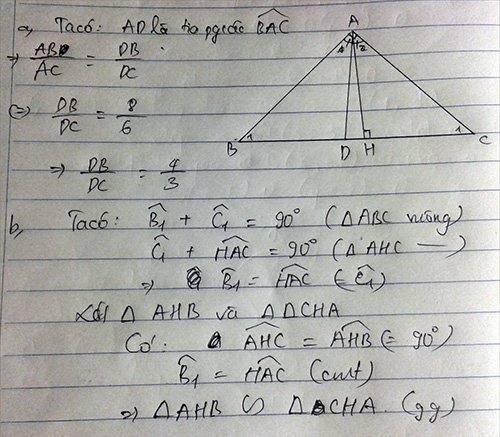
A B C D H 8cm 6cm
Giải
a) Xét\(\Delta AHB\)và\(\Delta BCD\)có:
\(\widehat{AHB}=\widehat{BCD}=90^o\)
\(\widehat{ABH}=\widehat{BDC}\) (so le trong)
=>\(\Delta AHB~\Delta BCD\) (g.g)
b) Xét\(\Delta AHD\)và\(\Delta AHB\)có:
\(\widehat{AHD}=\widehat{BHA}=90^o\)
\(\widehat{DAH}=\widehat{ABH}\)(cùng phụ\(\widehat{HAB}\))
=>\(\Delta AHD~\Delta AHB\) (g.g)
Mà ở cmt ta thấy\(\Delta AHB~\Delta BCD\)
Suy ra\(\Delta AHD~\Delta DCB\) (tính chất bắc cầu)
c) Áp dụng định lí Pi-ta-go vào tam giác vuông BCD có:
\(BD^2=BC^2+DC^2\)
\(BD^2=6^2+8^2\)
\(BD^2=36+64\)
\(BD=\sqrt{100}=10\left(cm,BD>0\right)\)
Xét tam giác vuông ABD có:
\(AH=\frac{AB.AD}{BD}=\frac{48}{10}=4,8\left(cm\right)\)
Áp dụng tính tính chất Pi-ta-go vào tam giác vuông AHB có:
\(AB^2=AH^2+HB^2\)
\(8^2=4,8^2+HB^2\)
\(HB^2=8^2-4,8^2\)
\(HB^2=40,96\)
\(HB=\sqrt{40,96}=6,4\left(cm,HB>0\right)\)
=> \(HD=BD-HB=10-6,4=3,6\left(cm\right)\)
Còn HC bn tự tính nhé!
#hoktot<3#