Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)

(P) có đỉnh I(1;1) và đi qua A(2;3) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{-b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=1\\a\cdot2^2+b\cdot2+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-4a\\4a+2b+c=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-2a\\4a+2\cdot\left(-2a\right)+c=3\\b^2-4ac=-4a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=3\\b=-2a\\4a^2-12a+4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=3\\4a^2-8a=0\\b=-2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}c=3\\4a\left(a-2\right)=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=3\\\left[{}\begin{matrix}a=0\left(loại\right)\\a=2\left(nhận\right)\end{matrix}\right.\\b=-2\cdot2=-4\end{matrix}\right.\)
=>c=3;a=2;b=-4
=>\(S=3^2+2^2+\left(-4\right)^2=25+4=29\)
=>Chọn C

- Từ các giả thiết của đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\-\dfrac{b}{2a}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\2a+3b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\\c=-1\end{matrix}\right.\)
Vậy hàm số trên có dạng : \(3x^2-2x-1=0\)

B(0;5) nằm trên đồ thị \((\)P\()\), ta có thể lập hệ phương trình sau:
2 = (-2)^2 + (-2b) + c 50^2 + Ob + c
Từ đó, ta có thể giải hệ phương trình để tìm giá trị của b và c
2=4-2b + c 5 = c
Vậy c = 5. Thay c vào phương trình đầu tiên, ta được:
2=4-2b+5
-7 = -2b
b = 7/2
Vậy đồ thị \((\)P\()\) của hàm số y = x^2 + (7/2)x + 5 là đường parabol mở lên, đi qua hai điểm A(-2;2) và B(0;5).
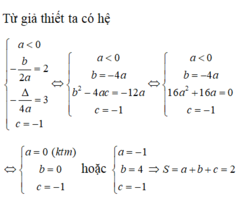
\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...