Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y = f(x) = \(\dfrac{12}{x}\)
a) f (5) = \(\dfrac{12}{5}=2.4\)
f (-3) = \(\dfrac{12}{-3}=-4\)
b)
| x | -6 | -4 | -3 | 2 | 5 | 6 | 12 |
|
y(x)=\(\dfrac{1}{2}\)x |
-3 | -2 | \(\dfrac{-3}{2}=-1,5\) | 1 | \(\dfrac{5}{2}=2,5\) | 3 | 6 |
Ta có: y=f(x)=12xy=f(x)=12x
a) f(5)=125=2,4f(5)=125=2,4
f(−3)=12−3=−4f(−3)=12−3=−4
b) Lần lượt thay bởi vào công thức ta được các giá trị tương ứng y là: .
Ta được bảng sau:
|
x |
-6 |
-4 |
-3 |
2 |
5 |
6 |
12 |
|
f(x)=12x |
-2 |
-3 |
-4 |
6 |
2,4 |
2 |
1 |

a) Điền số thích hợp vào ô trống:
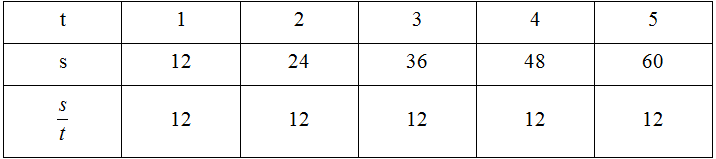
b) Hai đại lượng s và t tỉ lệ thuận vì s =12t, hệ số tỉ lệ bằng 12.

Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
x và y tỉ lệ thuận nên y = k.x
Từ đó ta tìm được y lần lượt là:
(-2).(-3) = 6 ; (-2) (-1) = 2;
(-2).1 = (-2) ; (-2).5 = -10
Ta được bảng sau
| x | -3 | -1 | 1 | 2 | 5 |
| y | 6 | 2 | -2 | -4 | -10 |

Vì x và y là hai đại lượng tỉ lệ nghịch nên x1y1 = x2y2 = x3y3 = …= a
Trong bảng x.y = 10.1,6 = 16. Từ đó ta có bảng sau:
|
x |
1 |
2 |
-4 |
6 |
-8 |
10 |
|
y |
16 |
8 |
-4 |
223223 |
-2 |
1,6 |

a) Vì với mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y , nên đại lượng y là hàm số của đại lượng x. b) Đại lượng y là hàm số của đại lượng x

a) Vì với mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y, nên đại lượng y là hàm số của đại lượng x.
b) Đại lượng y là hàm số của đại lượng x.
a) Vì mọi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.
b) Đại lượng y là hàm số của đại lượng x.

Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |
Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |
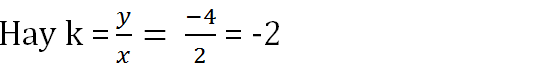
f (-3)=-5 f(6)=\(\dfrac{5}{2}\)
a)
y=f(x)
b) f(-3)=-5
f(6)=\(\dfrac{5}{2}\)