Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm của tiếp tuyến \(\Delta\) cần tìm
Ta có : \(y'=3x^2-12x+9\Rightarrow y'\left(x_0\right)=3x^2_0-12x_0+9\)
Ta có : \(x_0=1;y_0=2;y'\left(x_0\right)=0\)
Phương trình tiếp tuyến là : \(y-2=0\left(x-1\right)\) hay y = 2
b) Ta có \(x_0=0\Rightarrow y_0=-2,y'\left(x_0\right)=9\)
Phương trình tiếp tuyến là :\(y+2=9\left(x-0\right)\) hay \(y=9x-2\)
c) Ta có \(x_0=-1\Rightarrow y_0=f\left(x_0\right)=-18;y'\left(x_0\right)=24\)
Phương trình tiếp tuyến là : \(y+18=24\left(x+1\right)\) hay \(y=24x+6\)
d) Ta có : \(y_0=6\Rightarrow x_0^3-6x^2_0+9x_0-2=-2\Leftrightarrow x_0^3-6x^2_0+9x_0=0\)
\(\Leftrightarrow x_0=0;x_0=3\)
* \(x_0=-1\) suy ra phương trình tiếp tuyến là : \(y=9x-2\)
* \(x_0=3\Rightarrow y_0=-2,y'\left(x_0\right)=0\), suy ra phương trình tiếp tuyến là : \(y=2\)
Vậy có 2 tiếp tuyến là \(y=9x-2;y=2\)
e) Ta có : \(y'=0\Leftrightarrow\)\(\begin{cases}x=1\\x=3\end{cases}\)\(y''=6x-12\)
\(y''\left(1\right)=-6< 0;y"\left(3\right)=6>0\)
Suy ra đồ thị (C) có điểm cực tiểu là \(A\left(3;-2\right)\); điểm cực đại là \(B\left(1;2\right)\)
Giả sử \(M\left(a;a^3-6a^2+9a-2\right),a\ne3;1\)
Phương trình đường thẳng AB : \(2x+y-4=0\)
Ta có : \(S_{SBM}=\frac{1}{2}AB.d\left(M;AB\right)=6\)
\(\Leftrightarrow\frac{1}{2}\sqrt{2^2+\left(-4\right)^2}.\frac{\left|2a+a^3-6a^2+9a-2-4\right|}{\sqrt{2^2+1}}=6\)
\(\Leftrightarrow\left|a^3-6a^2+11a-6\right|=6\Leftrightarrow\left[\begin{array}{nghiempt}a=0\Rightarrow M\left(0;-2\right)\\a=4\Rightarrow M\left(4;2\right)\end{array}\right.\)
* Phương trình tiếp tuyến với (C) tại điểm M(0;-2) là : \(y+2=y'\left(0\right)\left(x-0\right)\) hay \(y=9x-2\)
* Phương trình tiếp tuyến với (C) tại điểm M(4;2) là : \(y-2=y'\left(4\right)\left(x-4\right)\) hay \(y=9x-34\)

a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)

Tập xác định : \(D=R\backslash\left\{1\right\}\)
Ta có \(y'=\frac{-1}{\left(x-1\right)^2}\).
Gọi \(M\left(x_o;y_0\right)\) là tiếp điểm
a) Ta có \(y_0=0\Rightarrow x_0=\frac{1}{2}\Rightarrow y'\left(x_0\right)=-4\)
Phương trình tiếp tuyến là : \(y=-4x+2\)
b) Phương trình hoành độ giao điểm của d và (C) :
\(\frac{2x-1}{x-1}=x+1\Leftrightarrow x^2-2x=0\Leftrightarrow x=0;x=2\)
* \(x_0=0\Rightarrow\) phương trình tiếp tuyến là : \(y=-x\left(x-0\right)+1=-x+1\)
* \(x_0=2\Rightarrow\) phương trình tiếp tuyến là : \(y=-x+5\)
c) Ta có phương trình của đường thẳng \(\Delta:y-\frac{2x_0-1}{x_0-1}=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0\right)\)
hay \(\Delta:\frac{1}{\left(x_0-1\right)^2}x+y-\frac{x_0}{\left(x_0-1\right)^2}-\frac{2x_0-1}{x_0-1}=0\)
Ta có : \(d\left(I;\Delta\right)=\frac{\left|\frac{2}{x_0-1}\right|}{\sqrt{\frac{1}{\left(x_0-1\right)^4}+1}}\le\sqrt{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\left(x_0-1\right)^4=1\Leftrightarrow\left[\begin{array}{nghiempt}x_0=0\\x_0=2\end{array}\right.\)
Suy ra có 2 tiếp tuyến là : \(\Delta_1:y=-x+1\)
\(\Delta_2:y=-x+5\)
d) Ta có : \(\Delta Ox=A\left(2x^2_0-2x_0+1;0\right)\)
\(OA=1\Leftrightarrow\left|2x^2_0-2x_0+1\right|=1\Leftrightarrow\left[\begin{array}{nghiempt}x_0=0\\x_0=1\end{array}\right.\)
Suy ra phương trình tiếp tuyến là : \(y=-x+1\)

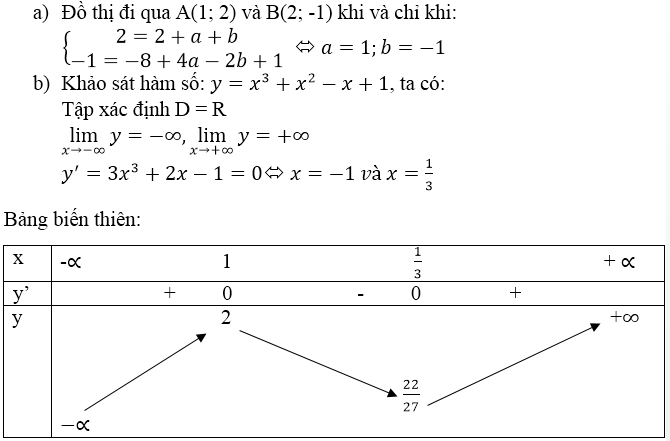
a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
Bảng biến thiên:
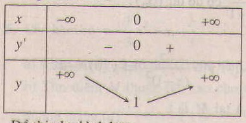
Đồ thị như hình bên.
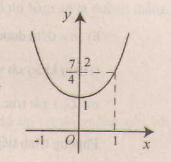
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.

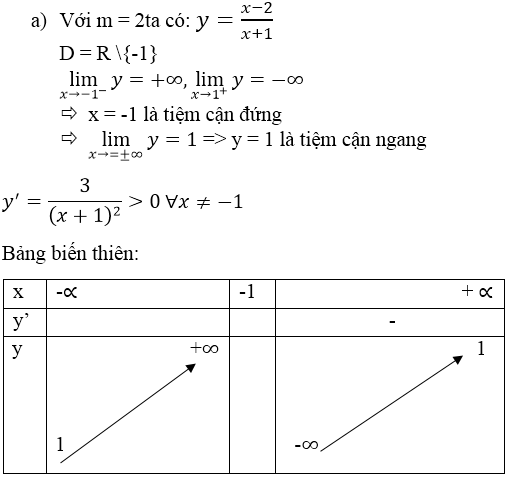
a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
Bảng biến thiên:
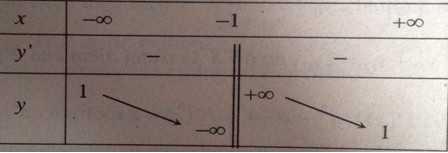
Đồ thị hàm số:
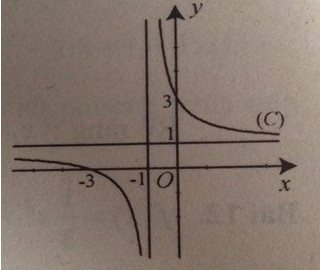
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).
TenAnh1
C = (-4.24, -6.16)
C = (-4.24, -6.16)
C = (-4.24, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
Vậy \(Min_{MN}=2\sqrt{3}\) khi \(m=3\).

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

Ta có \(y=x^4-4x^3+4x^2\Rightarrow4x^3-12x^2+8x\)
a. PTHD giao điểm của (C) và Parabol \(y=x^2\) :
\(x^4-4x^3+4x^2=x^2\Leftrightarrow x^2\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x=0;x=1;x=3\)
* \(x=0\) ta có phương trình tiếp tuyến là \(y=0\)
* \(x=2\) ta có phương trình tiếp tuyến là \(y=1\)
* \(x=3\) ta có phương trình tiếp tuyến là \(y=24x-63\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k \(\Rightarrow d:y=k\left(x-2\right)\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\left(2-x\right)^2x^2-k\left(x-2\right)\\4x\left(x-2\right)\left(x-1\right)=k\end{cases}\) có nghiệm
Thay k vào phương trình thứ nhất ta có :
\(x^4-4x^3+4x^2=\left(x-2\right)\left(4x^3-12x^2+8x\right)\)
\(\Leftrightarrow x\left(3x-4\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow x=0;x=2;x=\frac{4}{3}\)
* \(x=0\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)
* \(x=2\Rightarrow k=0\Rightarrow\) Phương trình tiếp tuyến \(y=0\)

a) (0 ; -1) ∈ (G) ⇔
b) m = 0 ta được hàm số có đồ thị (G0).
(HS tự khảo sát và vẽ đồ thị).
c) (G0) cắt trục tung tại M(0 ; -1). => y'(0) = -2.
Phương trình tiếp tuyến của (G0) tại M là : y - (-1) = y'(0)(x - 0) ⇔ y= -2x - 1.
\(y'=\dfrac{-3}{\left(x-2\right)^2}\)
d. Phương trình hoành độ giao điểm
\(\dfrac{x+1}{x-2}=x-\dfrac{1}{2}\Leftrightarrow2x^2-7x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Tại \(x=0\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{3}{4}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Pttt: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)
Tại \(x=\dfrac{7}{2}\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{4}{3}\\y=3\end{matrix}\right.\) tiếp tuyến: \(y=-\dfrac{4}{3}\left(x-\dfrac{7}{2}\right)+3\)
e.
Tam giác ABC là tam giác nào nhỉ? Có lẽ đó là tam giác OAB?
g.
Giao điểm (C) với Ox có tọa độ \(\left(-1;0\right)\)
\(\Rightarrow y'\left(-1\right)=-\dfrac{1}{3}\)
Phương trình tiếp tuyến:
\(y=-\dfrac{1}{3}\left(x+1\right)\)
h.
Giao điểm (C) với Oy có tọa độ \(\left(0;-\dfrac{1}{2}\right)\)
Chính là trường hợp đầu của câu d, phương trình: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)