Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
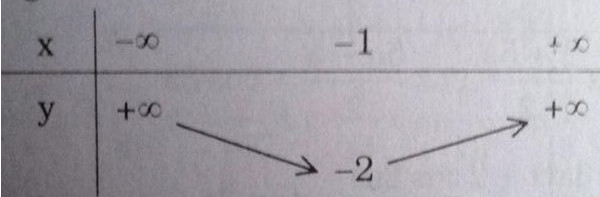
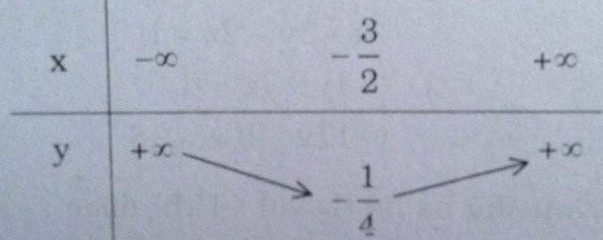
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
Đồ thị (C1) và (C2)
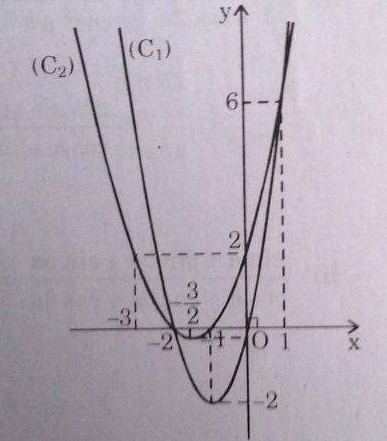
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)

\(-\frac{b}{2a}=-\frac{3}{2}\Leftrightarrow\frac{b}{2}=-\frac{3}{2}\Rightarrow b=-3\)
Phương trình (P): \(y=-x^2-3x+c\)
Thay tọa độ đỉnh \(x=-\frac{3}{2};y=\frac{1}{4}\) vào ta được:
\(\frac{1}{4}=-\frac{9}{4}+\frac{9}{2}+c\Rightarrow c=-2\)
\(\Rightarrow b+c=-5\)

\(a\ne0\)
Từ điều kiện đề bài ta có hệ:
\(\left\{{}\begin{matrix}c=-1\\-\frac{b}{2a}=2\\\frac{4ac-b^2}{4a}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=-1\\b=-4a\\-4a-b^2=0\end{matrix}\right.\) \(\Rightarrow b^2=b\Rightarrow\left[{}\begin{matrix}b=0\left(l\right)\\b=1\end{matrix}\right.\)
\(\Rightarrow a=-\frac{1}{4}\Rightarrow y=-\frac{1}{4}x^2+x-1\)

\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{3}{2}\\\frac{4ac-b^2}{4a}=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-b^2=a\end{matrix}\right.\) \(\Rightarrow4ac-9a^2=a\Rightarrow c=\frac{9a+1}{4}\)
Mặt khác theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=3\\x_1x_2=\frac{c}{a}=\frac{9a+1}{4a}\end{matrix}\right.\)
\(x_1^3+x_2^3=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=9\)
\(\Leftrightarrow27-9\left(\frac{9a+1}{4a}\right)=9\)
\(\Leftrightarrow12a-9a-1=4a\Rightarrow a=-1\)
\(\Rightarrow b=3\) ; \(c=-2\)
\(P=6\)

đồ thị hai hàm parabol có một điểm chung khi chúng có chung đỉnh
hay đỉnh I(1,3) của f(x) cũng là đỉnh của g(x)
dẫn đến giá trị nhỏ nhất của hai hàm là bằng nhau.
thế nên bài này sai ngay từ đề bài rồi nhé
hay nói cách khác , không tồn tại hai số a b thỏa mãn điều kiện trên
Do hàm có GTLN nên \(a< 0\)
Do ĐTHS đi qua A nên: \(a+b+c=-1\)
Hàm đạt GTLN tại \(x=-2\) nên \(-\frac{b}{2a}=-2\Leftrightarrow b=4a\)
\(\left\{{}\begin{matrix}\frac{b}{4}+b+c=-1\\a=\frac{b}{4}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\frac{b}{4}\\c=-\frac{5}{4}b-1\end{matrix}\right.\)
GTLN của hàm bằng 5 nên: \(\frac{4ac-b^2}{4a}=5\Leftrightarrow4ac-b^2=20a\)
\(\Rightarrow b\left(-\frac{5}{4}b-1\right)-b^2=5b\)
\(\Leftrightarrow-\frac{9}{4}b^2-6b=0\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow a=0\left(l\right)\\b=-\frac{8}{3}\end{matrix}\right.\)
\(\Rightarrow a=-\frac{2}{3}\) ; \(c=\frac{7}{3}\)
\(\Rightarrow25a-5b+c=...\)