Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) TXĐ: R
+) Với x \(\ne\) 1, f(x) = \(\frac{2x^2-x-1}{x-1}\) liên tục trên mỗi khoảng ( -\(\infty\); 1) và ( 1; +\(\infty\))
+) Với x = 1
Ta có: f(1) = 3
và \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\frac{2x^2-x-1}{x-1}=\lim\limits_{x\rightarrow1}\left(2x+1\right)=3\)
Vì f(1) = \(\lim\limits_{x\rightarrow1}f\left(x\right)\)
=> Hàm số f(x) liên tục tại điểm x = 1
Vậy f(x) liên tục trên R
b) TXĐ: R
+) Với x > 1
Có: f(x) = \(\frac{\sqrt{5x-1}-2}{x-1}\) liên tục trên ( 1; + \(\infty\))
+) Với x < 1
Có: f(x) = -6x + 5 liên tục trên ( - \(\infty\) ; 1 )
+) Với x = 1
f(1) = - 1
\(\lim\limits_{x\rightarrow1-}f\left(x\right)=\lim\limits_{x\rightarrow1-}\left(-6x+5\right)=-1\)
\(\lim\limits_{x\rightarrow1+}f\left(x\right)=\lim\limits_{x\rightarrow1+}\frac{\sqrt{5x-1}-2}{x-1}=\lim\limits_{x\rightarrow1+}\frac{5}{\sqrt{5x-1}+2}=\frac{5}{4}\)
Vì \(f\left(1\right)=\lim\limits_{x\rightarrow1-}f\left(x\right)\ne\lim\limits_{x\rightarrow1+}f\left(x\right)\)
=> f(x) gian đoạn tại x =1
Vậy: f(x) liên tục trên mỗi khoảng ( -\(\infty\); 1) và ( 1; +\(\infty\)) và gián đoạn tại x = 1

a/ \(\lim\limits_{x\rightarrow\sqrt{2}}f\left(x\right)=\lim\limits_{x\rightarrow\sqrt{2}}\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{2}}=\lim\limits_{x\rightarrow\sqrt{2}}\left(x+\sqrt{2}\right)=2\sqrt{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\sqrt{2}}f\left(x\right)=f\left(\sqrt{2}\right)\Rightarrow\) hàm số liên tục tại \(x=\sqrt{2}\)
b/ \(\lim\limits_{x\rightarrow5^+}f\left(x\right)=\lim\limits_{x\rightarrow5^+}\frac{x-5}{\sqrt{2x-1}-3}=\frac{\left(x-5\right)\left(\sqrt{2x-1}+3\right)}{2\left(x-5\right)}=\lim\limits_{x\rightarrow5^+}\frac{\sqrt{2x-1}+3}{2}=3\)
\(f\left(5\right)=\lim\limits_{x\rightarrow5^-}f\left(x\right)=\lim\limits_{x\rightarrow5^-}\left[\left(x-5\right)^2+3\right]=5\)
\(\Rightarrow\lim\limits_{x\rightarrow5^+}f\left(x\right)=\lim\limits_{x\rightarrow5^-}f\left(x\right)=f\left(5\right)\Rightarrow\) hàm số liên tục tại \(x=5\)

Bạn viết lại đề được ko? Ko hiểu \(\frac{x'+x}{x}\) với \(x\ne0\) là gì
Các câu dưới cũng có kí hiệu này, chắc bạn viết nhầm sang kí hiệu nào đó, nó cũng ko phải kí hiệu đạo hàm
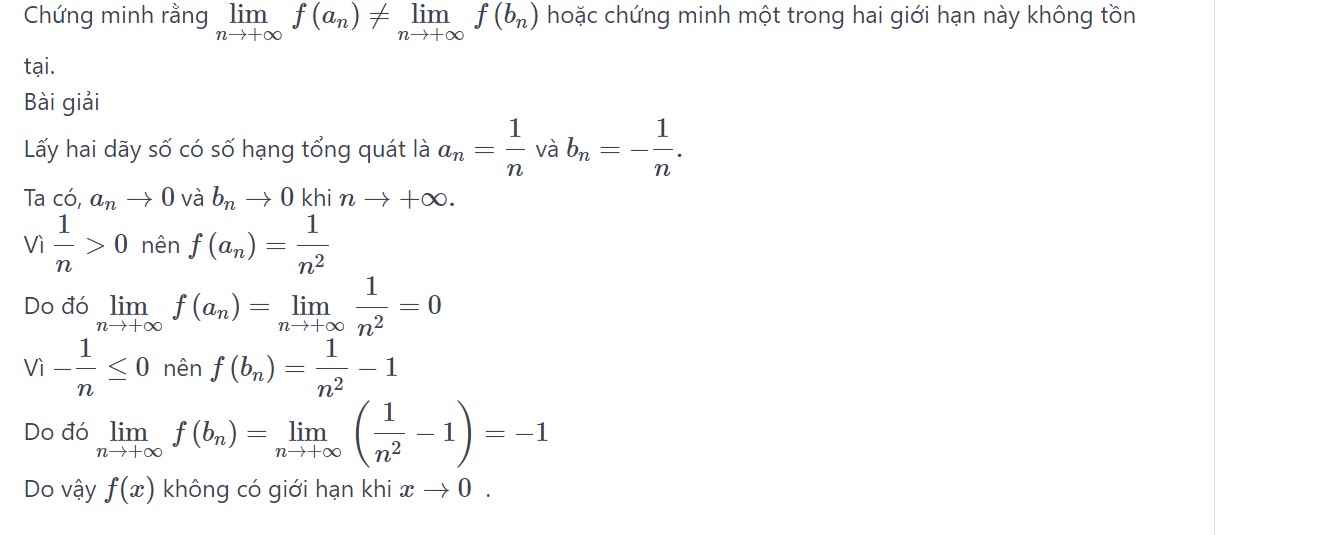
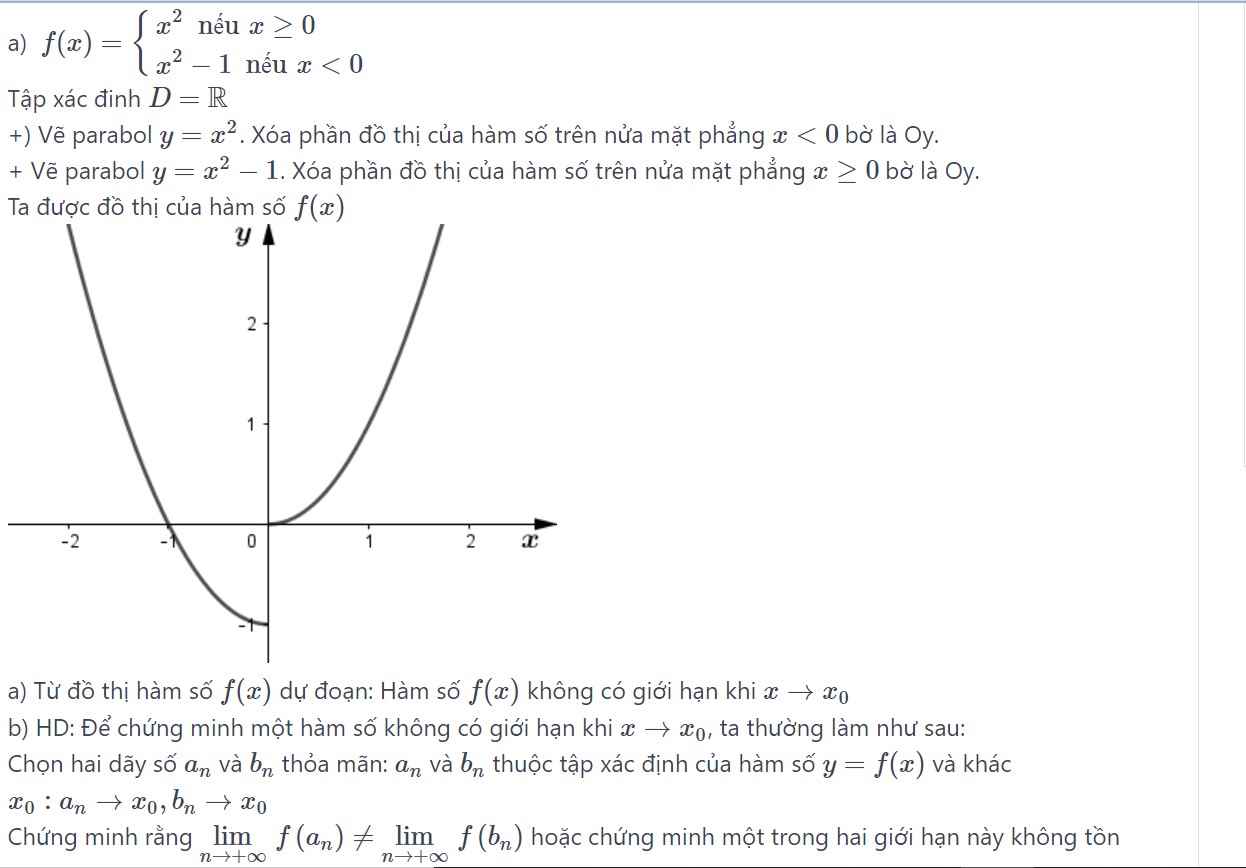
\(\lim\limits_{x\rightarrow1^-}=f\left(1\right)=\lim\limits_{x\rightarrow1^-}\sqrt{4-x^2}=\sqrt{3}\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(x^2+bx+c\right)=b+c+1\)
Để hàm số liên tục tại x=1 \(\Rightarrow b+c+1=\sqrt{3}\)
\(f'\left(1^-\right)=\lim\limits_{x\rightarrow1^-}\frac{-x}{\sqrt{4-x^2}}=-\frac{1}{\sqrt{3}}\)
\(f'\left(1^+\right)=\lim\limits_{x\rightarrow1^+}\left(2x+b\right)=b+2\)
Để hàm số có đạo hàm tại \(x=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+c+1=\sqrt{3}\\b+2=-\frac{1}{\sqrt{3}}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-2-\frac{1}{\sqrt{3}}\\c=1+\frac{4}{\sqrt{3}}\end{matrix}\right.\)
tìm b,c để hàm số có đạo hàm tại x=1