K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
1
CM
17 tháng 3 2018
Ta có:
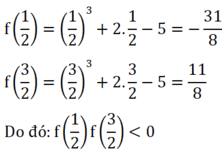
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên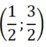 
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)
DA
0
CM
12 tháng 5 2018
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)
B
2
B
2
PT
31 tháng 3 2017
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.
31 tháng 3 2017
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.
\(log_5x=6;log_2x=1\)
\(\log_2\left(x+1\right)=8;\log_3\left(x^2+x+1\right)=2\)