Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn cách hack VIP OLM Vĩnh Viễn siêu dễ chỉ 10 phút là xong: youtube.com/watch?v=zYcnHqUcGZE&t

45 H B C D a, CM: \(\Delta AHB\)đồng dạng voi\(\Delta CAB\)
- Vì \(AH\perp BC\Rightarrow\widehat{AHB=90^o}\)
- Xét \(\Delta AHB\)và \(\Delta CAB\)có:
\(\widehat{AHB}=\widehat{BAC}\)
\(\widehat{A}\)chung
\(\Rightarrow\Delta AHB\)đồng dạng voi \(\Delta CAB\)(g-g) (đpcm)
b, CM: \(AC^2=CH.BC\)
- Xét \(\Delta AHC\)và \(\Delta BAC\)có:
\(\widehat{AHC}=\widehat{BAC}\left(=90^o\right)\)
\(\widehat{C}\)chung
\(\Rightarrow\Delta AHC\)đòng dạng với\(\Delta BAC\)(g-g)
\(\Rightarrow\frac{AC}{BC}=\frac{HC}{AC}\)
\(\Leftrightarrow AC^2=CH.BC\left(đpcm\right)\)

Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm

Cho a',b',c' là số đo cạnh của tam giác A'B'C'
a,b,c là số đo cạnh của tam giác ABC
a) Theo đề bài ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=k=\frac{3}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=\frac{a'+b'+c'}{a+b+c}=\frac{P_{A'B'C'}}{P_{ABC}}=k=\frac{3}{5}\)
Vậy tỉ số chu vi hai tam giác đã cho là 3/5
b) Chu vi tam giác ABC là: \(P_{ABC}=40:\left(5-3\right)\cdot5=100\left(dm\right)\)
Chu vi tam giác A'B'C' là: \(P_{A'B'C'}=P_{ABC}-40dm=100dm-40dm=60\left(dm\right)\)
A B C A' B' C'
a, Gọi CV tam giác A'B'C' là P', ABC là P
\(\Delta A'B'C'~\Delta ABC\)theo tỉ số đồng dạng \(k=\frac{3}{5}\)
\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=\frac{3}{5}\)
Áp dụng t/c DTSBN , ta có :
\(\frac{3}{5}=\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(=\frac{A'B'+B'C'+C'A'}{AB+BC+CA}=\frac{P'}{P}\)
Vậy tỉ số chu vi tam giác A'B'C' và ABC là \(\frac{3}{5}\)

A B C G M N P
a) Xét tg AGB có: M là trung điểm của GA (gt); N là trung điểm của GB (gt)
\(\Rightarrow\)MN là đường trung bình của tg \(\Rightarrow\)MN= 1/2 AB \(\Rightarrow\)MN/AB =1/2
CM tương tự: MP/AC =1/2 ; NP/BC =1/2
Xét tg MNP và tg ABC có: MN/AB =1/2 (cmt); MP/AC =1/2 (cmt); NP/BC =1/2 (cmt)
\(\Rightarrow\)tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2
b) tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2 \(\Rightarrow\)\(\frac{P\Delta MNP}{P\Delta ABC}=\frac{1}{2}\)mà \(P\Delta MNP=18cm\Rightarrow\)\(P\Delta ABC=\)2.18=36cm
(mk vẽ hình hơi xấu thông cảm nha)

Vì tam giác ABC đồng dạng với tam giác MNP nên;
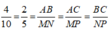
Theo tính chất dãy tỉ số bằng nhau ta có:
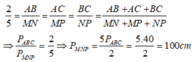
Chọn đáp án C

bài1
a) EF=??
b) không đồng dạng
c) không đồng dạng
d) Đồng dạng (vì sao thì bạn nhắn cho mình nha)
các cặp góc bằng nhau ABC=DEF; BCA=EFD; CAB=FDE
bài 2
a) theo tính chất đường trung bình trong mỗi tam giác (không hiểu thì nhắn cho mình)
ta có MN=1/2AB => MN/AB=1/2 (1)
NM=1/2BC => NP/BC=1/2 (2)
MP=1/2AC => MP/AC=1/2 (3)
từ (1),(2),(3) => MNP đồng dạng với ABC
b) vì MNP đồng dạng với ABC với tỉ số k là 2 ( theo câu a)
nên chu vi ABC = 2 lần chu vi MNP =40cm
Do tam giác ABC đồng dạng với tam giác MNP nên:
Theo tính chất của dãy tỉ số bằng nhau ta có:
Vậy
Chọn đáp án A