Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O x y z m n t t'
Tự đánhgóc
Có xOy < xOz (40 < 120)
=> Oy nằm giữa Ox,Oz
=> xOy + yOz = xOz
=> yOz = 40o
Om là p/g xOy
=> mOx = mOy = xOy/2 = 20o
On là p/g xOz
=> nOx = zOn = xOz/2 = 60o
Có xOm < xOn (20 < 60)
=> Om nằm giữa On và Ox
=> xOm + mOn = xOn
=> mOn = 40o
Có mOy < mOn ( 20<40)
=> Oy nằm giữa Om, On
=> mOy + yOn = mOn
=> yOn = 20o
Vì yOn = mOn = 20o
Oy nằm giữa Om,On
=> Oy là p/g của mOn
chetme làm vội quên câu cuối
c) Ot là tia đối tia Ox
=> tOn và xOn kề bù
=> tOn + nOx = 180o
=> tOn = 120o
Ot' là tia đối Oz
=> zOn và t'On kề bù
=> zOn + t'On = 180o
=> t'On = 120o
=> t'On = tOn

O x z y m 1 2
Giải: Vì Oz nằm giữa Ox và Oy nên góc xOz + góc zOy = góc xOy
=> góc zOy = góc xOy - góc xOz = 800 - 300 = 500
Do Om là tia p/giác của góc yOz nên, ta có:
góc O1 = góc O2 = góc zOy/2 = 500/2 = 250
Vì Oz nằm giữa Ox và Om nên góc xOz + góc zOm = góc xOm
=> góc xOm = 300 + 250 = 550
Vậy góc xOm = 550

Theo bài ra ta có hình vẽ :
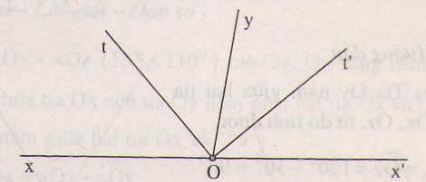
O x y z x' t' t
a) Trên cùng nửa mặt phẳng bờ chứa tia Ox có \(\widehat{xOz}< \widehat{xOy}\left(30^o< 80^o\right)\)nên tia Oz nằm giữa hai tia Ox và Oy
\(\Rightarrow\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
hay \(30^o+\widehat{yOz}=80^o\)
\(\Rightarrow\widehat{yOz}=80^o-30^o=50^o\)
b) Vì Ot là tia phân giác của \(\widehat{xOz}\)
\(\Rightarrow\widehat{xOt}=\widehat{tOz}=\frac{\widehat{xOz}}{2}=15^o\)
Vì Ox' là tia Ox là hai tia đối nhau
\(\Rightarrow\widehat{x'Ox}=180^o\)
Vì \(\widehat{x'Oz}< \widehat{x'Ox}\)nên tia Oz nằm giữa hai tia Ox' và Ox
\(\Rightarrow\widehat{x'Oz}+\widehat{xOz}=\widehat{x'Ox}\)
hay \(\widehat{x'Oz}+30^o=180^o\)
\(\Rightarrow\widehat{x'Oz}=150^o\)
Vì Ot' là tia phân giác của \(\widehat{x'Oz}\)
\(\Rightarrow\widehat{x'Ot'}=\widehat{t'Oz}=\frac{\widehat{x'Oz}}{2}=75^o\)
Vì \(\widehat{tOz}< \widehat{zOt'}\)nên tia Oz nằm giữa hai tia Ot và Ot'
\(\Rightarrow\widehat{tOz}+\widehat{t'Oz}=\widehat{t'Ot}\)
hay \(15^o+75^o=\widehat{t'Ot}\)
\(\Rightarrow\widehat{t'Ot}=90^o\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có xÔy > xÔz ( 80 * > 30*)
nêm tia Oz nằm giửa 2 tia Oy và Ox
suy ra xÔy + yÔz = xÔy
30* + yÔz = 80*
yÔz = 80* - 30* = 50*
b)phần b dài lắm , chờ bạn khác giải nhá

Giải:
Hai góc xOy và x'Oy là hai góc kề bù mà = 1000 nên
= 1800 - 1000 = 800.
Giải tương tự bài 33, ta được ,

1) Trên cùng nửa mặt phẳng bờ OA, ta có \(\widehat{AOB}< \widehat{AOC}\)nên OB nằm giữa OA, OC, suy ra \(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)
OD là phân giác \(\widehat{AOB}\)nên AD nằm giữa OA, OB, suy ra \(\widehat{AOD}+\widehat{DOB}=\widehat{AOB}\). Ngoài ra, \(\widehat{AOD}=\widehat{DOB}< \widehat{AOB}\)
\(\widehat{AOD}< \widehat{AOB};\widehat{AOB}< \widehat{AOC}\Rightarrow\widehat{AOD}< \widehat{AOC}\).
Trên cùng nửa mặt phẳng bờ OA, ta có \(\widehat{AOD}< \widehat{AOC}\)nên OD nằm giữa OA,OC, suy ra \(\widehat{AOD}+\widehat{DOC}=\widehat{AOC}\)
\(\Leftrightarrow\widehat{AOD}+\widehat{DOC}=\widehat{AOB}+\widehat{BOC}\Leftrightarrow\widehat{AOD}+\widehat{DOC}=\widehat{AOD}+\widehat{DOB}+\widehat{BOC}\)
\(\Leftrightarrow\widehat{DOC}=\widehat{DOB}+\widehat{BOC}\Leftrightarrow\) OB nằm giữa OD, OC
2) \(\frac{\widehat{COB}+\widehat{COA}}{2}=\frac{\widehat{COB}+\widehat{AOD}+\widehat{DOB}+\widehat{BOC}}{2}=\frac{2\left(\widehat{COB}+\widehat{DOB}\right)}{2}=\widehat{COD}\)
Phân giác của 2 góc kề bù là 1 góc vuông
tOt' = 90 độ