
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



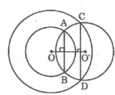
Vì đường tròn (O’) cắt đường tròn (O ; OA) tại A và B nên OO’ là trung trực của AB
Suy ra : OO’ ⊥ AB (1)
Vì đường tròn (O’) cắt đường tròn (O ; OC) tại C và D nên OO’ là trung trực của CD
Suy ra : OO’ ⊥ CD (2)
Từ (1) và (2) suy ra : AB // CD.

O B A E C d D I G F
a) Gọi d là tiếp tuyến tại A của đường tròn (O) => d vuông góc OA => d vuông góc AB
Vì AB là đường kính của đường tròn (AB) nên d cũng là tiếp tuyến của (AB)
Vậy (O) và (AB) tiếp xúc nhau tại A (đpcm).
b) Gọi I là trung điểm đoạn AB => I là tâm của (AB) => ^ICA = ^IAC = ^OEA => IC // OE
Ta thấy OB = BI = IA = OA/3 => \(\frac{AI}{AO}=\frac{1}{3}\). Áp dụng ĐL Thales vào \(\Delta\)AEO có
\(\frac{AC}{AE}=\frac{AI}{AO}=\frac{1}{3}\) => AC = 1/3.AE (1)
Gọi OC,OD cắt đường tròn (O) cho trước lần lượt tại F,G. Khi đó DC // GF
Hay GF // AE. Mà GF và AE là các dây của đường tròn (O) nên (GE = (AF => ^EOG = ^AOF
Xét \(\Delta\)ODE và \(\Delta\)OCA: OD = OC, ^EOD = ^AOC (cmt), OE = OA => \(\Delta\)ODE = \(\Delta\)OCA (c.g.c)
=> ED = AC. Kết hợp với (1) suy ra AC = DE = AE/3 => AC = CD = DE (đpcm).


∆ ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ ABC vuông tại C
CO = OA = (1/2)AB (tính chất tam giác vuông)
AC = AO (bán kính đường tròn (A))
Suy ra: AC = AO = OC
∆ ACO đều góc AOC = 60 °
∆ ADB nội tiếp trong đường tròn đường kính AB nên ∆ ADB vuông tại D
DO = OB = OA = (1/2)AB (tính chất tam giác vuông)
BD = BO(bán kính đường tròn (B))
Suy ra: BO = OD = BD
∆ BOD đều


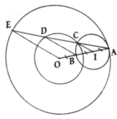
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE